Actions mécaniques, forces et inertie
Introduction :
Ce cours traite des actions mécaniques qui existent entre les objets ou systèmes.
Dans un premier temps, nous définirons les actions mécaniques et mettrons en évidence les différents types d’actions qui existent.
Puis nous verrons comment modéliser les actions mécaniques exercées sur un système ou objet par un diagramme objet-actions.
Nous aborderons ensuite la notion de force exercée sur un système pour représenter une action mécanique.
Enfin, nous énoncerons le principe d’inertie, règle fondamentale que suivent les forces exercées sur un objet ou système.
Les différentes actions mécaniques
Les différentes actions mécaniques
Définition
Action mécanique :
Lorsqu’un objet ou système agit sur un autre objet, on parle d’action mécanique.
Une action mécanique exercée sur un système a des effets sur celui-ci :
- elle peut déformer le système ;
- elle peut mettre le système en mouvement si celui-ci était immobile ;
- elle peut modifier le mouvement du système, et même l’arrêter.
Définition
Action de contact :
Si les systèmes ou objets qui agissent l’un sur l’autre sont en contact, on parle d’action de contact. L’action mécanique de contact est répartie sur toute la surface de contact et s’arrête s’il n’y a plus de contact.
Exemple
L’action du vent sur une voile, l’action de l’air sur un parachute ou l’action d’un marteau sur un clou par exemple, sont des actions mécaniques de contact.
Définition
Action à distance :
Si les systèmes ou objets qui agissent l’un sur l’autre sont à distance, on parle d’action à distance.
Exemple
Le poids d’un système par exemple est l’action mécanique à distance exercée par la Terre sur ce système. Elle est toujours à prendre en compte dans l’étude d’un système.
Les forces électriques, magnétiques et nucléaires sont d’autres exemples d’actions à distance.
Pour modéliser une action mécanique, on définit le système qui exerce l’action et le système qui la subit. Un objet ou système étudié peut être soumis à plusieurs actions mécaniques.
On peut représenter les différentes actions mécaniques exercées sur un système ou objet par un diagramme objet-actions.
Diagramme objet-actions
Diagramme objet-actions
La construction du diagramme objet-actions suit plusieurs étapes :
- Première étape, on fait la liste des objets ou systèmes qui agissent entre eux.
- Deuxième étape, on schématise les différents objets ou systèmes. En suivant des normes :
- le nom du système étudié est écrit dans une ellipse d’une certaine couleur ;
- autour de ce cercle, on inscrit les noms des autres systèmes dans des ellipses d’une couleur différente.
- Troisième étape, on schématise par des flèches les actions mécaniques exercées sur le système étudié.
Le sens de la flèche va du système qui exerce l’action vers le système étudié. Là encore il y a des normes de représentation :
- une action de contact est représentée par une flèche en trait plein ;
- une action à distance est représentée par une flèche en pointillés.
Exemple
Voici le bilan des actions mécaniques qui s’exercent sur un ballon posé sur le sol au moment où le joueur tape dedans :
Pied tapant dans un ballon
Le système étudié est le ballon, il est inscrit dans une ellipse orange (voir schéma ci-dessous). Les systèmes exerçant une force sur le ballon sont inscrits dans des ellipses bleues. Il y en a trois :
- le pied du joueur qui exerce sur le ballon une action mécanique de contact. L’action est représentée par une flèche en trait plein dirigée vers le ballon ;
- la pelouse qui exerce sur le ballon une action mécanique de contact. L’action est représentée par une flèche en trait plein dirigée vers le ballon ;
- la Terre exerce sur le ballon une action mécanique à distance. L'action est représentée par une flèche en pointillés dirigée vers le ballon.
Forces exercées sur un système
Forces exercées sur un système
Principes de représentation
Principes de représentation
Définition
Vecteur de force :
Une force exercée sur un système peut être représentée par un vecteur force F caractérisé par un point d’application, une direction ou droite d’action, un sens et une valeur exprimée en Newtons N.
Astuce
Les vecteurs sont des segments fléchés. Ils ont une direction, celle du segment, et un sens, celui de la flèche. Ils ont aussi une « longueur » mais pour un vecteur on parle de norme.
À retenir
Deux forces se compensent si elles ont même direction, même valeur et des sens opposés.
Définition
Point d'application :
Le point d’application de la force se situe au point de contact entre le système étudié et le système qui exerce la force s’il s’agit d’une action mécanique de contact.
Exemple
Dans l’exemple du tir dans le ballon, le point d’application est le point de contact entre le pied et le ballon. C’est de là que part le vecteur représentant la force exercée.
Définition
Droite d'action :
On appelle droite d’action la droite qui a la même direction que la force et qui passe par son point d’application.
La Terre quant à elle exerce sur le système une action mécanique à distance et dans ce cas-là, le point d’application de la force se situe au centre de gravité du système étudié.
À retenir
Pour nommer les vecteurs sur le schéma du système, on indique en indice le système qui exerce la force et le système étudié. $$\overrightarrow{F}_{système/système\ étudié}$$
Compte tenu du diagramme objet-action, on sait qu’il y a en tout trois forces qui s’exercent sur le système :
- le pied du joueur exerce une force de contact $\overrightarrow F$ sur le ballon ; $$\overrightarrow{F}_\text{pied/ballon}$$
- la pelouse exerce elle aussi une force de contact ; $$\overrightarrow{F}_\text{pelouse/ballon}$$
- en revanche, l’action terrestre se fait à distance, l’origine du vecteur est donc le centre de gravité du ballon. $$\overrightarrow{F}_\text{Terre/ballon}$$
Interpréter les actions des forces représentées
Interpréter les actions des forces représentées
Connaissant la direction et le sens d’une force, on peut prévoir son action sur le système.
Considérons un système en mouvement sur lequel s’exerce une force :
- Premier cas : la force est parallèle à la direction du mouvement. Elle peut alors modifier la vitesse du mouvement. En effet si la force est parallèle et dans le même sens que le mouvement, elle accélère celui-ci.
Par contre si elle est parallèle et en sens opposé au mouvement, elle ralentit celui-ci.
- Deuxième cas : la force est perpendiculaire à la direction du mouvement. Elle peut alors modifier la trajectoire du mouvement. En effet si la force est perpendiculaire au mouvement et dirigée vers le haut, alors elle peut dévier la trajectoire vers le haut.
Et inversement si la force est perpendiculaire au mouvement et dirigée vers le bas, elle peut dévier la trajectoire vers le bas.
- Troisième cas : la force est orientée de façon quelconque (ni parallèle ni perpendiculaire au mouvement). Elle peut alors modifier à la fois la vitesse et la trajectoire du mouvement.
Le poids
Le poids
Attention
Dans le schéma précédent, toutes les forces étaient symbolisées par le vecteur F, mais en réalité, certaines forces ont des notations qui leurs sont propres.
À retenir
Ainsi, la force à distance qu’exerce la Terre sur tout système ou objet posé sur elle ou présent dans son champ d’action est appelé le poids et est notée vecteur $\overrightarrow{P}$. $$\overrightarrow{P}_\text{Terre/système}$$
Les caractéristiques du poids $\overrightarrow{P}$ d’un système sont les suivantes :
- puisque c’est une action mécanique à distance, son point d’application est le centre de gravité du système ;
- sa direction est verticale, orientée vers le centre de la Terre ;
- son sens est vers le bas ;
- sa valeur est exprimée en Newton N ; le poids se calcule en multipliant la masse du système par l’intensité de pesanteur. $$P= m\times g$$ où $m$ est la masse du système en kilogrammes kg. $g$ est l’intensité de la pesanteur, c’est une constante sur Terre où elle vaut 9,81 newtons par kilogramme N.Kg-1.
Exemple
Prenons l’exemple d’une skieuse tirée par un remonte-pente et faisons le bilan des forces qui s’exercent sur elle, en considérant que les frottements des skis sur la neige sont négligeables.
Astuce
On précise toujours le système étudié et le référentiel d’étude avant de faire le bilan des forces.
Ici le système étudié est la skieuse et on se trouve dans un référentiel terrestre.
Passons au bilan des forces :
- La première est le poids P, noté $\overrightarrow{P}_\text{Terre/skieuse}$
Ses caractéristiques sont :
- le point d’application : ici le centre de gravité G de la skieuse ;
- la direction : elle est verticale ;
- le sens : le vecteur est orienté vers le bas ;
- la valeur : P qui est égale à m×g est exprimée en newtons N $$P=m\times g$$ Dans cette formule, $m$ est la masse de la skieuse en kilogrammes et $g$ est l’intensité de pesanteur (soit 9,81 N.kg-1).
- L’autre force qui s’exerce est la force de traction $\overrightarrow{T}_{perche/skieuse}$ de la perche du remonte-pente :
- son point d’application est le point de contact A entre la skieuse et la perche ;
- sa direction est inclinée d’un angle β par rapport à l’horizontale ;
- son sens est orienté vers le haut ;
- sa valeur est T, exprimée en newtons N.
- La troisième et dernière force est la force de réaction de la piste, notée $\overrightarrow{R}_{piste/skieuse}$ :
- son point d’application est le point de contact B entre la skieuse et la pente ;
- sa direction est perpendiculaire à la pente ;
- son sens est orienté vers le haut ;
- sa valeur est R, exprimée en Newton N.
Principe d’inertie
Principe d’inertie
Définition
Système :
Un système est dit isolé quand il n’est soumis à aucune force extérieure : il n'interagit pas avec son environnement.
Un système est dit pseudo-isolé quand il est soumis à des forces qui se compensent.
À retenir
Principe physique d’inertie :
Si dans le référentiel terrestre, un système n’est soumis à aucune force ou est soumis à des forces qui se compensent, alors soit ce système reste immobile soit il a un mouvement rectiligne uniforme (c’est à dire que sa trajectoire est une droite et sa vitesse est constante).
Réciproquement, si dans le référentiel terrestre, un système est immobile ou a un mouvement rectiligne uniforme, alors les forces qui s’exercent sur ce système se compensent.
Si on l’étudie généralement dans un référentiel terrestre, le principe d’inertie s’applique aussi dans les autres référentiels :
- dans le référentiel géocentrique il sert à étudier le mouvement de la Lune ou des satellites.
- dans le référentiel héliocentrique il permet d’étudier le mouvement des planètes.
Pour étudier plus en détails le principe d’inertie, prenons l’exemple d’une valise qui se déplace sur un tapis roulant et faisons le bilan des forces qui s’exercent sur elle.
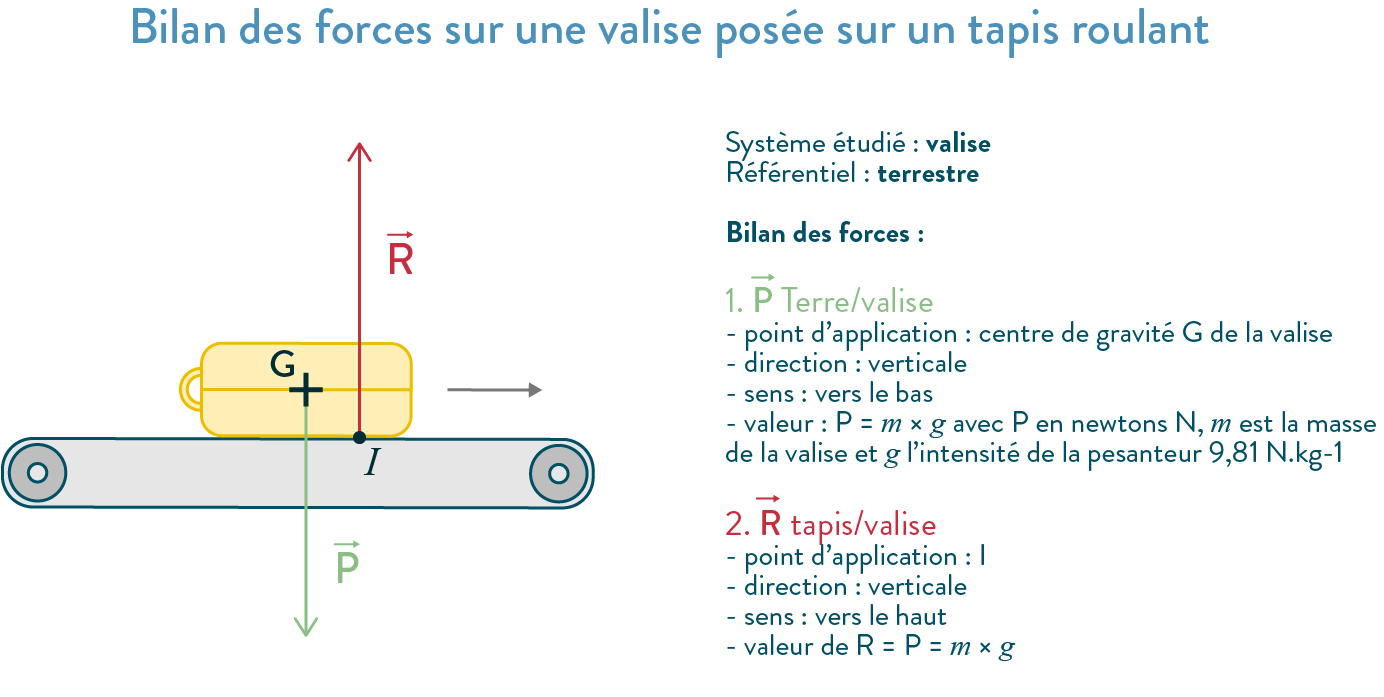
Le système étudié est la valise, dans un référentiel terrestre.
À présent effectuons le bilan des forces en présence :
- Tout d’abord le poids $\overrightarrow{P}_\text{Terre/valise}$ :
- son point d’application est le centre de gravité G de la valise ;
- il a une direction verticale ;
- son sens est vers le bas ;
- sa valeur est $P= m\times g$ exprimée en newtons N où $m$ est la masse de la valise et $g$ l’intensité de la pesanteur $9,81\ \text{N} \cdot \text{kg}^{-1}$.
- La seconde force qui entre en jeu est la réaction du tapis roulant $\overrightarrow{R}_\text{tapis/valise}$.
Comme la valise a un mouvement rectiligne uniforme, sa trajectoire est une droite et elle avance à vitesse constante sur le tapis. Donc, d’après le principe de l’inertie, les forces qui s’exercent sur la valise se compensent.
Donc le poids $\overrightarrow{P}_\text{Terre/valise}$ et la réaction $\overrightarrow{R}_\text{tapis/valise}$ ont la même direction, la même valeur et sont de sens opposés.
- Comme le poids est toujours vertical et dirigé vers le bas, on en déduit les caractéristiques de la réaction $\overrightarrow{R}_\text{tapis/valise}$ :
- le point d’application est le point de contact entre la valise et le tapis roulant ;
- la direction suis une droite verticale ;
- le sens est vers le haut ;
- la valeur de R est égale à la valeur de P et est donc elle aussi égale à $m\times g$.