Cours Additionner ou soustraire des fractions
Pourquoi apprendre à additionner ou soustraire des fractions ?
- Parce que les fractions sont des nombres que l’on peut utiliser dans la vie de tous les jours (pour parler de durées par exemple : on dit « une demi-journée », « un quart d’heure », etc.).
Comme tous les nombres, on peut les additionner ou les soustraire lorsqu’on fait des calculs.
Additionner ou soustraire des fractions qui ont le même dénominateur
Additionner ou soustraire des fractions qui ont le même dénominateur
Rappel
Le numérateur est au-dessus de la barre de fraction et le dénominateur est en-dessous.
À retenir
Quand deux fractions ont le même dénominateur, on additionne ou on soustrait uniquement les deux numérateurs entre eux.
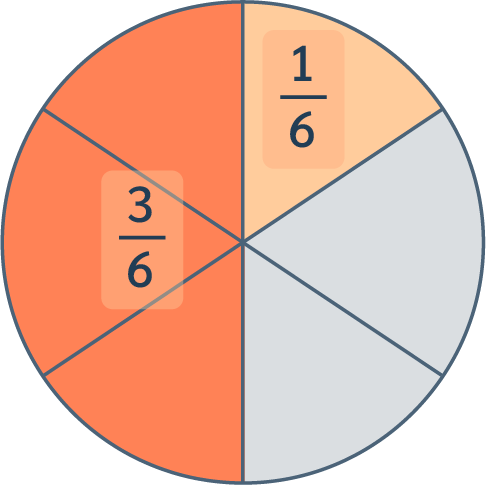
Exemple d’addition : $$\dfrac{1}{6}+\dfrac{3}{6}$$ On peut additionner $\dfrac{1}{6}+\dfrac{3}{6}$ car le dénominateur est le même : c’est 6 !
- On garde donc le même dénominateur.
- On additionne simplement les numérateurs entre eux : $1+3=4$.
Ainsi, on a : $\dfrac{1}{6}+\dfrac{3}{6}=\dfrac{4}{6}$
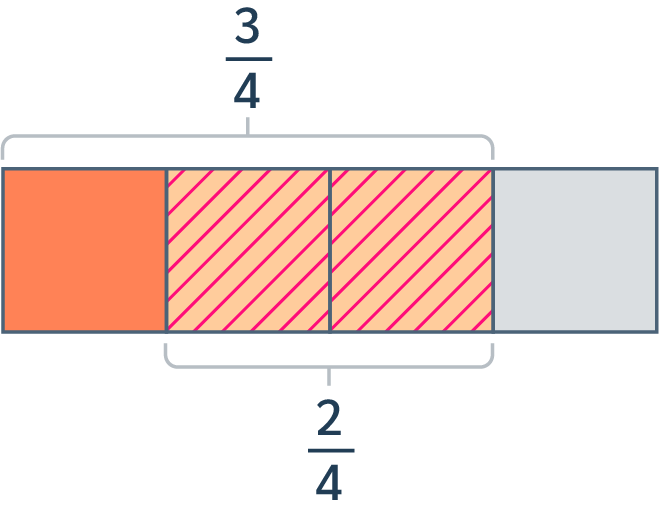
Exemple de soustraction : $$\dfrac{3}{4}-\dfrac{2}{4}$$
3/4 - 2/4 On peut soustraire $\dfrac{3}{4}-\dfrac{2}{4}$ car le dénominateur est le même : c’est 4 !
- On garde donc le même dénominateur.
- On soustrait simplement les numérateurs entre eux : $3-2=1$.
Ainsi, on a : $\dfrac{3}{4}-\dfrac{2}{4}=\dfrac{1}{4}$
Rappel
Si lors du calcul, le résultat est une fraction dont le numérateur est égal au dénominateur, alors la fraction vaut 1.
Exemple : $$\dfrac{3}{4}+\dfrac{1}{4}=\dfrac{4}{4}$$ On sait que $\dfrac{4}{4}=1$.
Donc $\dfrac{3}{4}+\dfrac{1}{4}=1$.
Additionner ou soustraire des fractions dont les dénominateurs sont différents
Additionner ou soustraire des fractions dont les dénominateurs sont différents
À retenir
Si on veut additionner ou soustraire des fractions dont les dénominateurs ne sont pas les mêmes, il faut tout d’abord se servir des égalités de fraction.
Ainsi, on pourra obtenir deux fractions qui ont le même dénominateur et donc faire l’addition ou la soustraction.
Exemple d’addition : $$\dfrac{1}{3}+\dfrac{3}{6}$$
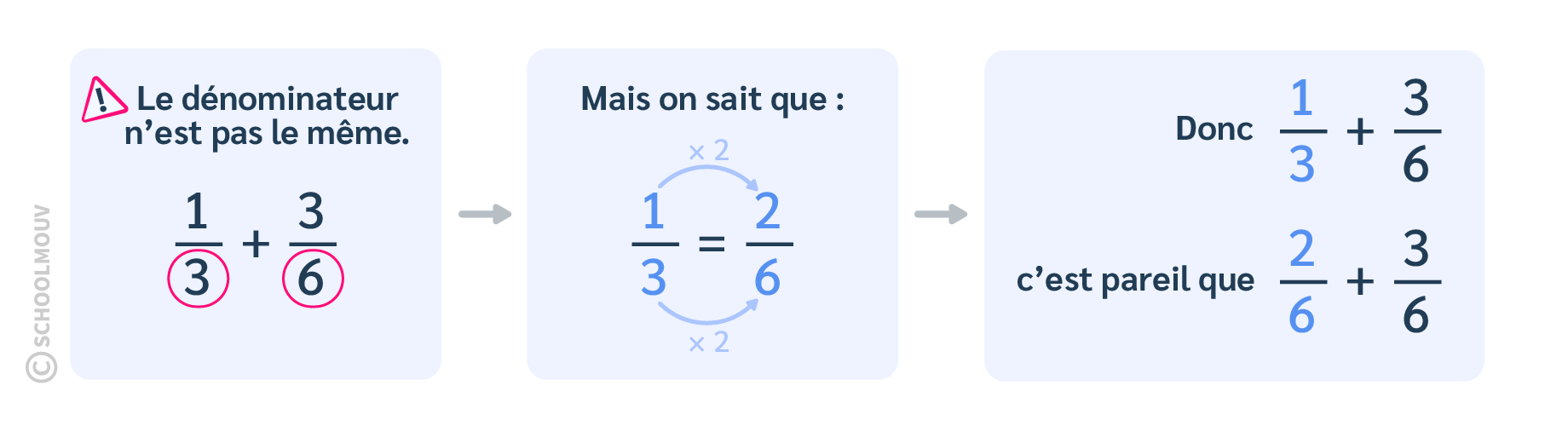
Maintenant on peut calculer : $\dfrac{2}{6}+\dfrac{3}{6}=\dfrac{5}{6}$.
On sait donc calculer : $\dfrac{1}{3}+\dfrac{3}{6}=\dfrac{5}{6}$.
Exemple de soustraction : $$\dfrac{5}{8}-\dfrac{1}{4}$$
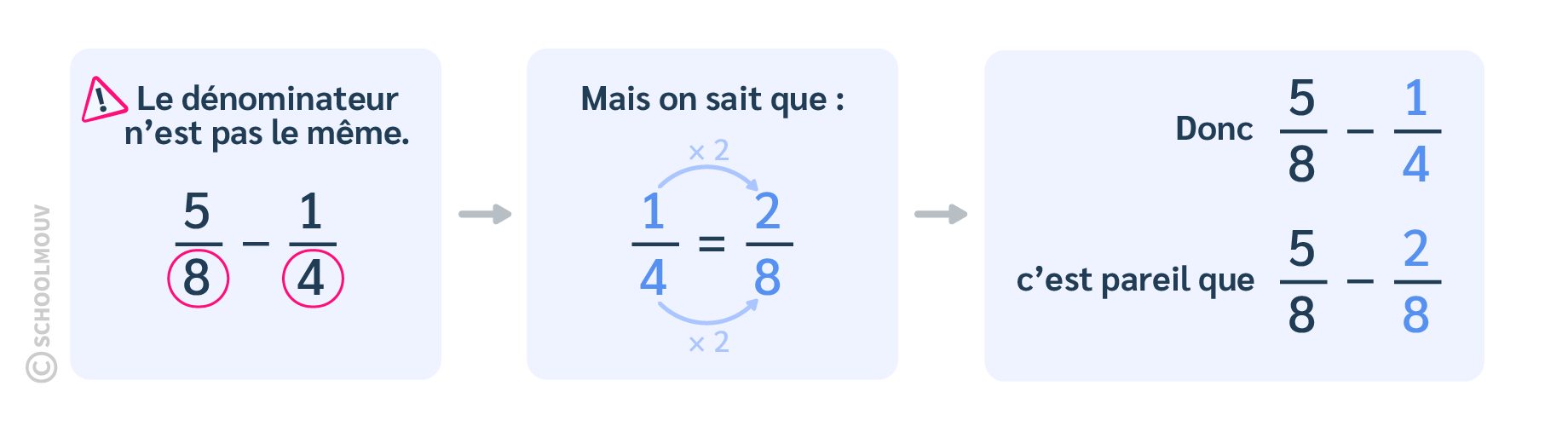
Maintenant on peut calculer : $\dfrac{5}{8}-\dfrac{2}{8}=\dfrac{3}{8}$.
On sait donc calculer : $\dfrac{5}{8}-\dfrac{1}{4}=\dfrac{3}{8}$.