Convertir des unités de grandeurs simples
Introduction :
Pour pouvoir comparer des grandeurs de même nature entre elles, les additionner, les soustraire ou tout simplement donner un résultat dans une unité de mesure spécifique, il faut très souvent changer d’unités.
Ce cours portera sur les techniques de conversions des grandeurs simples, et nous nous attarderons plus spécifiquement sur la grandeur temps qui nécessite une approche un peu différente.
Définition
Convertir une grandeur :
Convertir une grandeur, c’est écrire cette grandeur soit dans un autre système d’unités, soit à l’aide d’un multiple ou d’un sous-multiple de l’unité de départ.
Règles générales
Règles générales
La plupart des grandeurs simples (hors grandeur temps) sont exprimées dans le système d’unités décimal (base $10$) et peuvent donc être converties à l’aide du tableau ci-dessous qui indique des multiples et des diviseurs de l’unité.
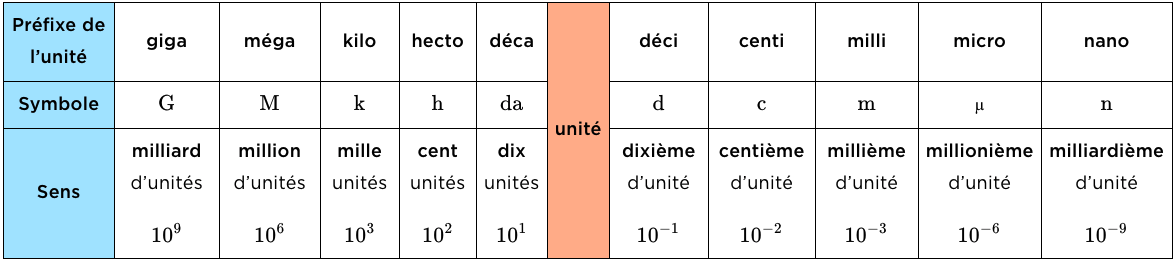
MÉTHODOLOGIE
- On écrit le nombre de départ dans le tableau de conversion ci-dessus en veillant à bien inscrire le chiffre des unités de ce nombre dans la colonne de l’unité de départ.
- Le nombre d’arrivée est le nombre obtenu en positionnant la virgule sur le bord droit de la colonne de l’unité d’arrivée.
Astuce
Si besoin, les colonnes vides peuvent être remplies d’un $0$.
Exemple
On veut convertir $3\ 185,9\text{ m}$ en $\text{km}$ puis en $\text{cm}$.
Le tableau de conversions des longueurs nécessaire ici est le suivant.
| $\text{km}$ | $\text{hm}$ | $\text{dam}$ | $\text m$ | $\text{dm}$ | $\text{cm}$ | $\text{mm}$ |
On écrit $31\ 859$ en positionnant le $\blue 5$ dans la colonne des $\blue{\text m}$.
| $\text{km}$ | $\text{hm}$ | $\text{dam}$ | $\blue{\text m}$ | $\text{dm}$ | $\text{cm}$ | $\text{mm}$ |
| $3$ | $1$ | $8$ | $\blue 5$ | $9$ |
Pour obtenir la conversion en $\text{km}$, on positionne la virgule sur le bord droit de la colonne des $\red{\text{km}}$.
| $\red{\text{km}}$ | $\text{hm}$ | $\text{dam}$ | $\text m$ | $\text{dm}$ | $\text{cm}$ | $\text{mm}$ |
| $3\ \Large{\red{\text{,}}}$ | $1$ | $8$ | $5$ | $9$ |
- On obtient $3\red{,}1859\text{ km}$.
Pour obtenir la conversion en $\text{cm}$, on positionne la virgule sur le bord droit de la colonne des $\purple{\text{cm}}$.
| $\text{km}$ | $\text{hm}$ | $\text{dam}$ | $\text m$ | $\text{dm}$ | $\purple{\text{cm}}$ | $\text{mm}$ |
| $3$ | $1$ | $8$ | $5$ | $9$ | $\purple{0\ \Large{{\text{,}}}}$ |
- On obtient $31\ 859\purple{0}\text{ cm}$.
Spécificités de quelques grandeurs
Spécificités de quelques grandeurs
- La plus grande unité de longueur généralement utilisée est le kilomètre, noté $\text{km}$. On parle ensuite de milliers, millions ou milliards de kilomètres.
- La plus grande unité de masse généralement utilisée est la tonne, notée $\text t$, qui est le nom commun du mégagramme ($1\text{ t} = 10^6\text{ g} = 10^3\text{ kg}$). On parle ensuite de milliers, millions ou milliards de tonnes.
- La plage d’unités d’intensité la plus courante va du kiloampère (noté $\text{kA}$) au milliampère (noté $\text{mA}$).
- La plage d’unités de tension la plus courante va du mégavolt (noté $\text{MV}$) au volt ($\text{V}$).
- La plage d’unités de puissance la plus courante va du gigawatt (noté $\text{GW}$) au milliwatt (noté $\text{mW}$).
Cas particulier de la grandeur temps
Cas particulier de la grandeur temps
La grandeur temps est très souvent exprimée dans le système d’unités sexagésimal (base $60$).
- On sait déjà convertir des heures en minutes : on multiplie par $60$.
- On sait également convertir des minutes en secondes : on multiplie par $60$.
- On sait donc convertir des heures en secondes : on multiplie par $3\ 600$.
Pour les opérations inverses, c'est-à-dire pour passer de minutes en heures et de secondes en minutes, il suffira donc de diviser la valeur initiale par $60$.
Dans la vie courante, nous utilisons très souvent des conversions comme $\frac 14$ d’heure pour $15$ minutes, $\frac 12$ heure pour $30$ minutes, $\frac 34$ d’heure pour $45$ minutes…
On peut ainsi déjà établir un tableau de proportionnalités avec des valeurs connues, tableau qui nous permettra d’établir rapidement des conversions pour des valeurs plus complexes.
Ainsi :
- $\color{#76C663}{50}$ minutes valent $\color{#EE6A58}{\frac{50}{60}}$ d’heure soit $50\text{ min} \approx 0,833\text{ h}$.
- $\color{#76C663}{25}$ secondes valent $\color{#EE6A58}{\frac{25}{60}}$ de minute soit $25\text{ s} \approx 0,417\text{ min}$.
- $\color{#76C663}{25}$ secondes valent aussi $\frac{25}{60\times 60}=\color{#EE6A58}{\frac{25}{3\ 600}}$ d’heure soit $25\text{ s} \approx 0,007\text{ h}$.
On a aussi :
- $2\text{ h}\ 30\text{ min} = 2\text{ h} + 0,5\text{ h} = 2,5\text{ h}$
- $3\text{ h}\ 50\text{ min} \approx 3\text{ h} + 0,833\text{ h} \approx 3,833\text{ h}$
- $1\text{ h}\ 15\text{ min}\ 25\text{ s} \approx 1\text{ h} + 0,25\text{ h} + 0,007\text{ h} \approx 1,257\text{ h}$
Conclusion :
Ce cours est évidemment très important car on utilise fréquemment la conversion d’unités pour ajouter, soustraire ou comparer des grandeurs de même nature entre elles. Il faut donc maintenant parfaitement maîtriser la conversion des grandeurs simples afin de pouvoir aborder sereinement la conversion des grandeurs composées.