Géométrie : éléments de base

En géométrie, on utilise des codes simples et précis pour tracer, nommer et reconnaître les figures.
Dans cette leçon, nous allons voir ce que sont les points, les droites, les segments, les angles et leurs particularités. Nous verrons également les principaux codes utilisés pour bien lire et tracer des figures géométriques.

Point, segment, droite et demi-droite

Le point

Le point est la plus petite unité en géométrie.

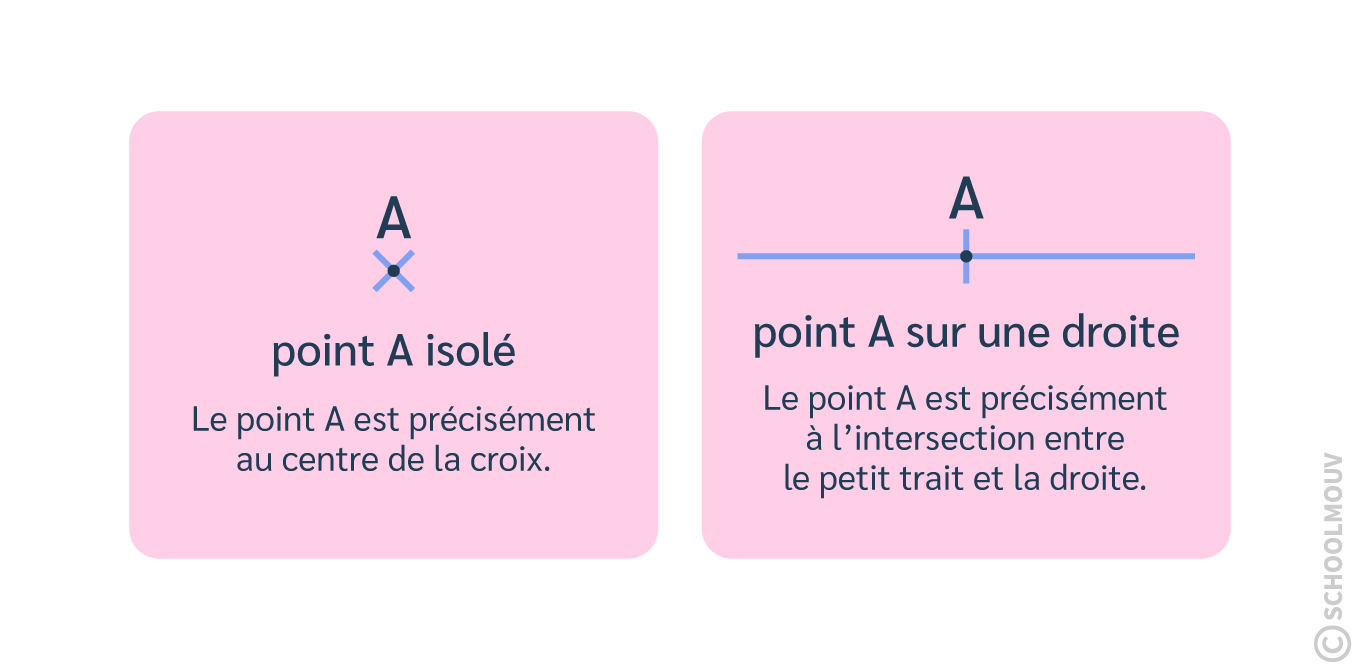
On le nomme par une lettre majuscule (A, B, C, etc.) et il est souvent représenté par une croix (lorsqu’il est isolé) ou par un petit trait (lorsqu’il est sur une droite).

Définition

Intersection :

Une intersection de deux droites, c’est leur croisement en un point.

La droite

La droite est formée par un nombre infini de points alignés.
Elle n’a ni début, ni fin.

On nomme une droite par une lettre minuscule notée entre parenthèses.
Les parenthèses représentent l’infini de la droite.

Deux droites sécantes sont des droites qui se coupent en un point.

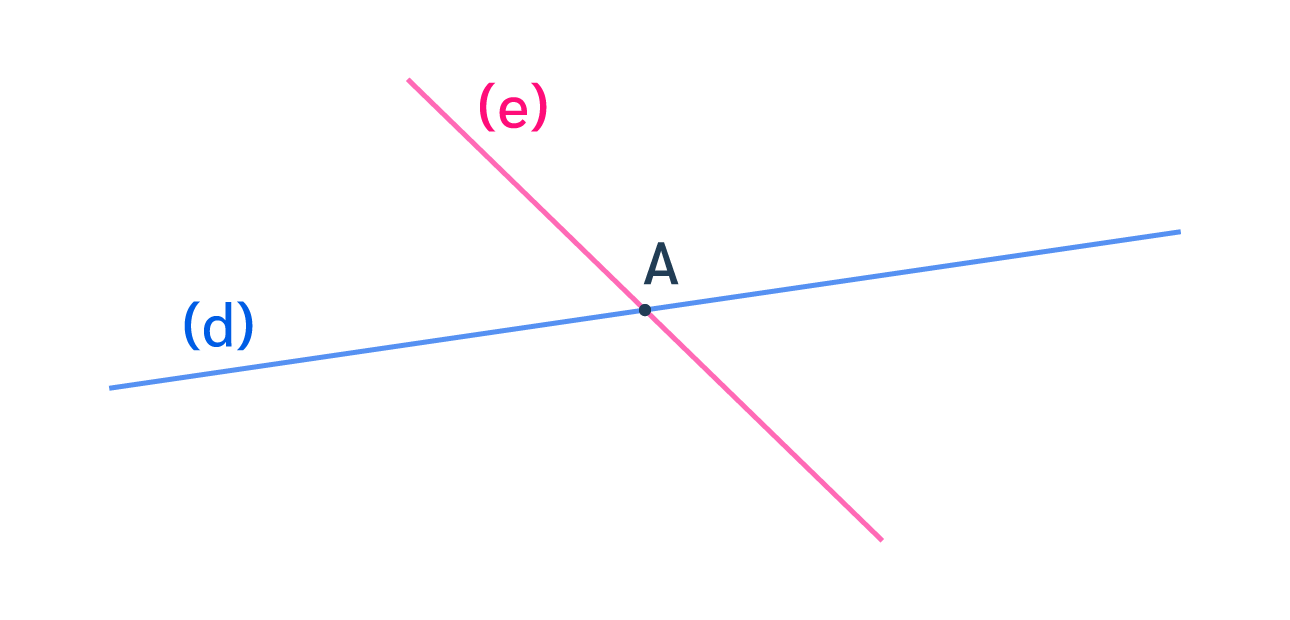
• Ici, les deux droites (d) et (e) sont sécantes en A.

Le segment

Un segment est une partie d’une droite, comprise entre deux points.
Contrairement à la droite, il est donc limité : il a un début et une fin.

On nomme un segment par les deux lettres des points qui la limitent notés entre crochets.
Les crochets représentent les limites précises du segment.

• Ici, le segment [BC] est bien délimité.
  On peut imaginer qu’il est sur une droite qui se poursuit (pointillés).

Le milieu d’un segment se trouve à égale distance des deux extrémités : il partage le segment en deux parties de même longueur.

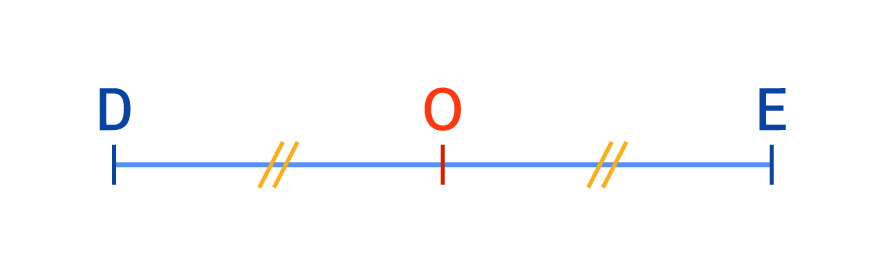
• Ici, le point O est le milieu du segment [DE].
  Le point O étant le milieu de [DE], les segments [DO] et [OE] sont de même longueur : on indique cette égalité par un symbole identique (ici, deux petits traits).

Astuce

Lorsque l’on a plusieurs segments et que certains ont une même longueur, on peut utiliser plusieurs symboles pour repérer les longueurs identiques :

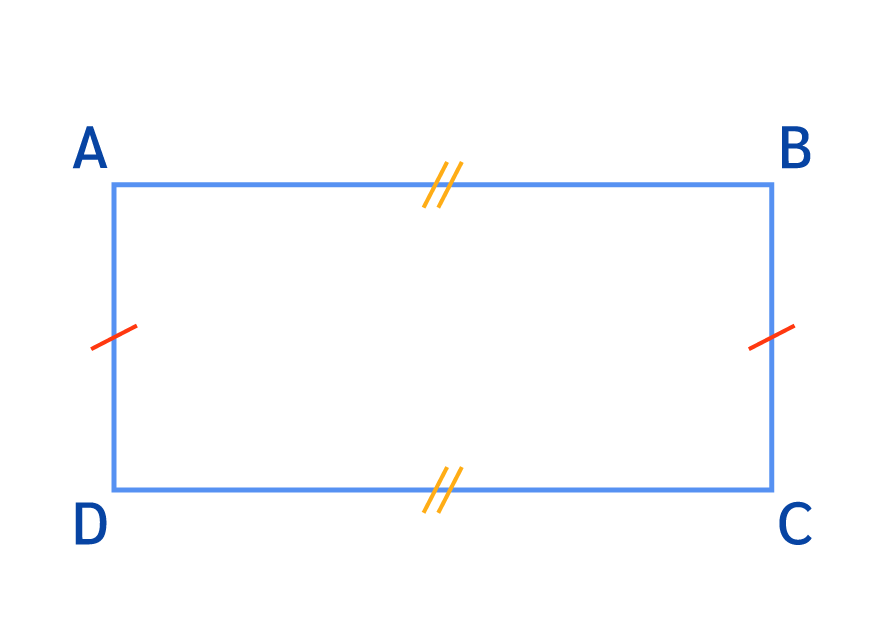
• Dans le rectangle ABCD, les deux côtés opposés sont de même longueur, on peut représenter cette égalité par un même symbole :
  → symbole avec deux traits : AB = DC
  → symbole avec un trait : AD = BC.

Attention

Lorsqu’on parle de segments, on met des crochets, mais lorsqu’on parle de longueurs (mesures), alors on ne met aucun crochet.
Ainsi, dans le rectangle ABCD, les segments [AB] et [DC] sont de même longueur. On pourra dire que AB = DC (sous-entendu la longueur AB est égale à la longueur DC).

La demi-droite

Une demi-droite a pour origine un point précis et se prolonge à l’infini dans une seule direction : elle a un début (un point de départ), mais pas de fin.

On nomme une demi-droite par la lettre de son point de départ et la lettre d’un point qu’elle traverse, en mettant un crochet du côté de son origine et une parenthèse du côté infini.

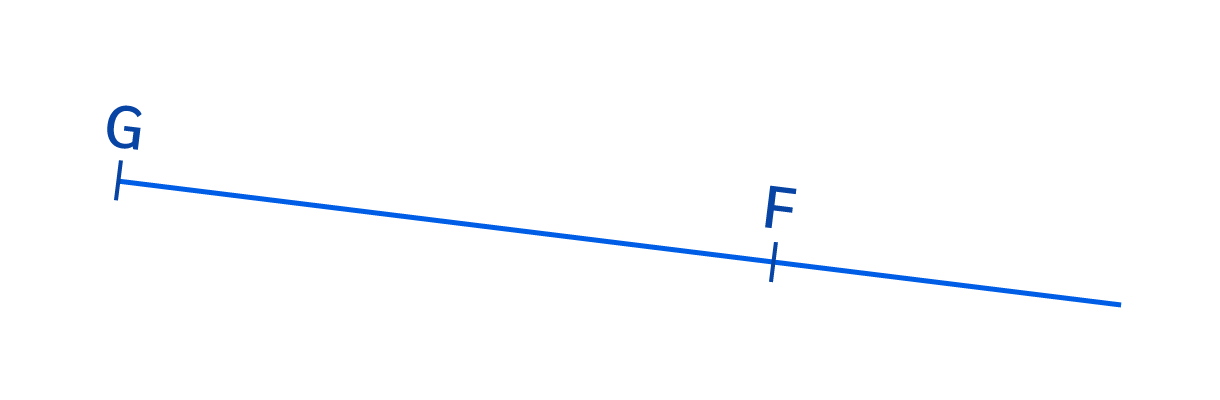
• Ici, la demi-droite [GF) a pour origine le point G et passe par le point F (elle continue après F).

Les angles

Un angle est formé de deux demi-droites qui ont la même origine (le même point de départ).
Cette origine est alors le sommet de l’angle.
Les demi-droites forment les côtés de l’angle.

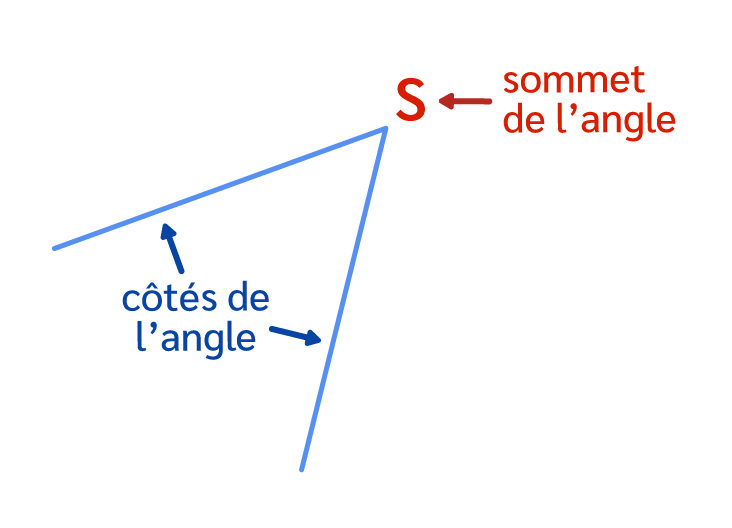
• Ici, les deux demi-droites ont pour origine le point S et elles forment les côtés de l’angle.

L’angle droit

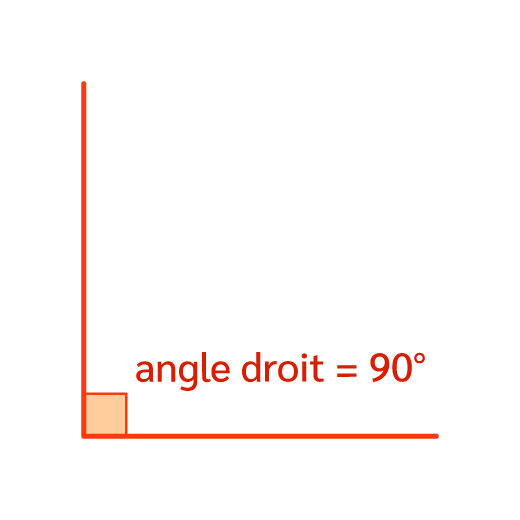
Un angle droit est un angle qui mesure 90°.
On peut le repérer à l’aide d’une équerre.

On note un angle droit ainsi :

L’angle obtus

Un angle obtus est un angle qui mesure plus de 90°.
Il est donc plus grand qu’un angle droit.

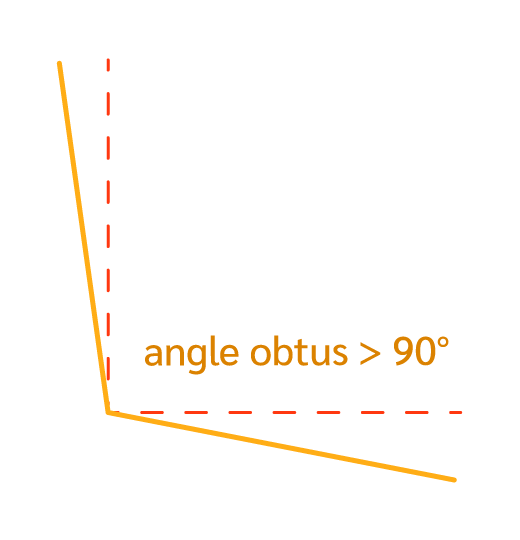
• Ici, l’angle bleu est plus grand que 90°. C’est donc bien un angle obtus.

L’angle aigu

Un angle aigu est un angle qui mesure moins de 90°.
Il est donc plus petit qu’un angle droit.

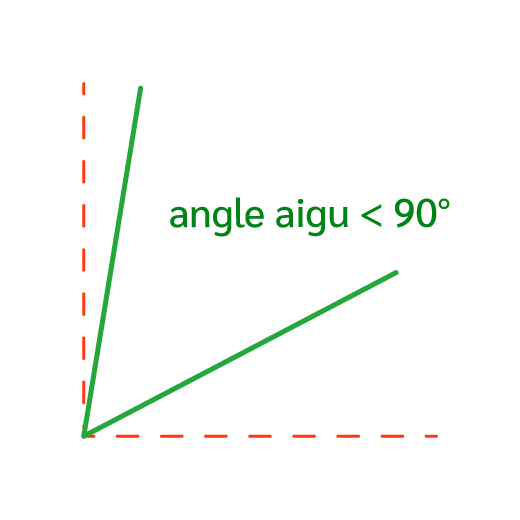
• Ici, l’angle vert est plus petit que 90°. C’est donc bien un angle aigu.

Les instruments utilisés en géométrie

• La règle est un outil géométrique qui sert à mesurer des longueurs et à tracer des lignes droites.

• L’équerre est un outil géométrique en forme de triangle rectangle qui permet de repérer et tracer des angles droits.

• Le compas est un outil géométrique qui permet de tracer des cercles ou des arcs de cercle. Il permet également de reporter une longueur ou de mesurer une distance entre deux points.