Mémoriser les faits numériques en calcul mental

Pré-requis :

• Connaitre les tables d’addition et de multiplication
• Connaitre la notion de double, moitié, multiple
• Connaitre la notion de nombre décimal

Dans cette leçon, nous allons aborder quelques résultats en calcul mental qu’il est important de connaître par cœur, ainsi que quelques astuces pour mieux les mémoriser.

Calcul mental avec des nombres entiers

Pour calculer plus vite, sans avoir besoin de poser les opérations, il est utile de connaître par cœur certains faits numériques.

Rappel

Voici quelques rappels pour commencer :

• Les doubles des nombres de 1 à 20 :

Le double de 1	2
Le double de 2	4
Le double de 3	6
Le double de 4	8
Le double de 5	10
Le double de 6	12
Le double de 7	14
Le double de 8	16
Le double de 9	18
Le double de 10	20

Le double de 11	22
Le double de 12	24
Le double de 13	26
Le double de 14	28
Le double de 15	30
Le double de 16	32
Le double de 17	34
Le double de 18	36
Le double de 19	38
Le double de 20	40

• Les moitiés des nombres pairs de 2 à 40 :

La moitié de 2	1
La moitié de 4	2
La moitié de 6	3
La moitié de 8	4
La moitié de 1	5
La moitié de 12	6
La moitié de 14	7
La moitié de 16	8
La moitié de 18	9
La moitié de 20	10

La moitié de 22	11
La moitié de 24	12
La moitié de 26	13
La moitié de 28	14
La moitié de 30	15
La moitié de 32	16
La moitié de 34	17
La moitié de 36	18
La moitié de 38	19
La moitié de 40	20

• Les doubles de certains nombres entre 20 et 90 :

• Les doubles de certains nombres entre 100 et 1 000 :

Astuce

Si tu connais le double de 20, alors tu connais aussi le double de 200 : il suffit de multiplier par 10 !
Le double de 20 est 40.
Donc, le double de 200 ($20\times\mathbf{10}$) est 400 ($40\times\mathbf{10}$).
On ajoute simplement un zéro !

Il en va de même pour tous les doubles de nombres que tu viens de voir.
Exemples :

• Le double de 25 est 50.
  Donc, le double de 250 ($25\times\mathbf{10}$) est 500 ($50\times\mathbf{10}$).
• Le double de 25 est 50.
  Donc, le double de 250 ($25\times\mathbf{10}$) est 500 ($50\times\mathbf{10}$).
• Le double de 14 est 28.
  Donc, le double de 140 ($14\times\mathbf{10}$) est 280 ($28\times\mathbf{10}$).

• Les moitiés de dizaines entières :

• Les moitiés de centaines entières :

Astuce

Les moitiés sont l’inverse des doubles !
Si tu as mémorisé les doubles, tu connais donc les moitiés.
Exemples :

• Le double de 17 est 34.
  Donc, la moitié de 34 est 17.
• Le double de 75 est 150.
  Donc, la moitié de 150 est 75.

• Les multiples de 25 :

$$25\times 1=25$$ $$25\times 2=50$$ $$25\times 3=75$$ $$25\times 4=100$$

Rappel

Un multiple d’un nombre est le résultat d’une multiplication de ce nombre par un nombre entier.
Exemples :

• 50 est bien un multiple de 25, car il est le résultat de la multiplication de 25 par 2 ;
• 30 est bien un multiple de 10, car il est le résultat de la multiplication de 10 par 3 ;
• 12 est bien un multiple de 4, car il est le résultat de la multiplication de 4 par 3…

• Les décompositions multiplicatives de 60 :

$$\mathbf{60=}$$ $$60\times 1$$ $$30\times 2$$ $$20\times 3$$ $$15\times 4$$ $$6\times 10$$

La mémorisation de ces faits numériques te permet de compléter des opérations à trous directement grâce au calcul mental.
Exemples :

• $2\times …=30$
• $2\times 16=…$
• $2\times …=70$
• $1\,000=2\times …$

Calcul mental avec des fractions

Certaines fractions simples sont faciles à comparer, à additionner ou à soustraire de tête, sans poser de calculs.

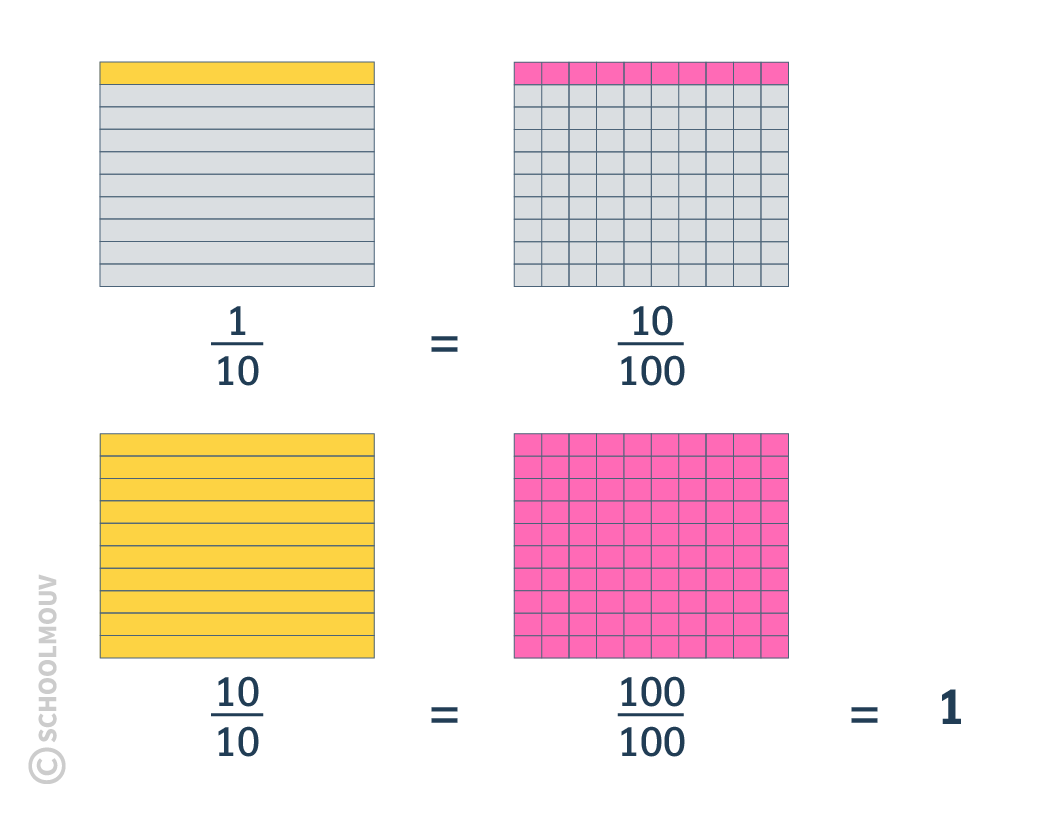
• Fractions de nombres entiers :

Rappel

Lorsque le numérateur et le dénominateur d’une fraction sont le même nombre, alors cette fraction est égale à 1.
Exemple :

Il faut se souvenir que l’on peut établir des relations entre les fractions.
Exemple :

En CM1, tu deviens capable de comparer, additionner, soustraire des fractions de nombres entiers, en utilisant directement le calcul mental.
Exemple :

• Fractions décimales :

Les fractions décimales peuvent être représentées de différentes façons.
Exemples :

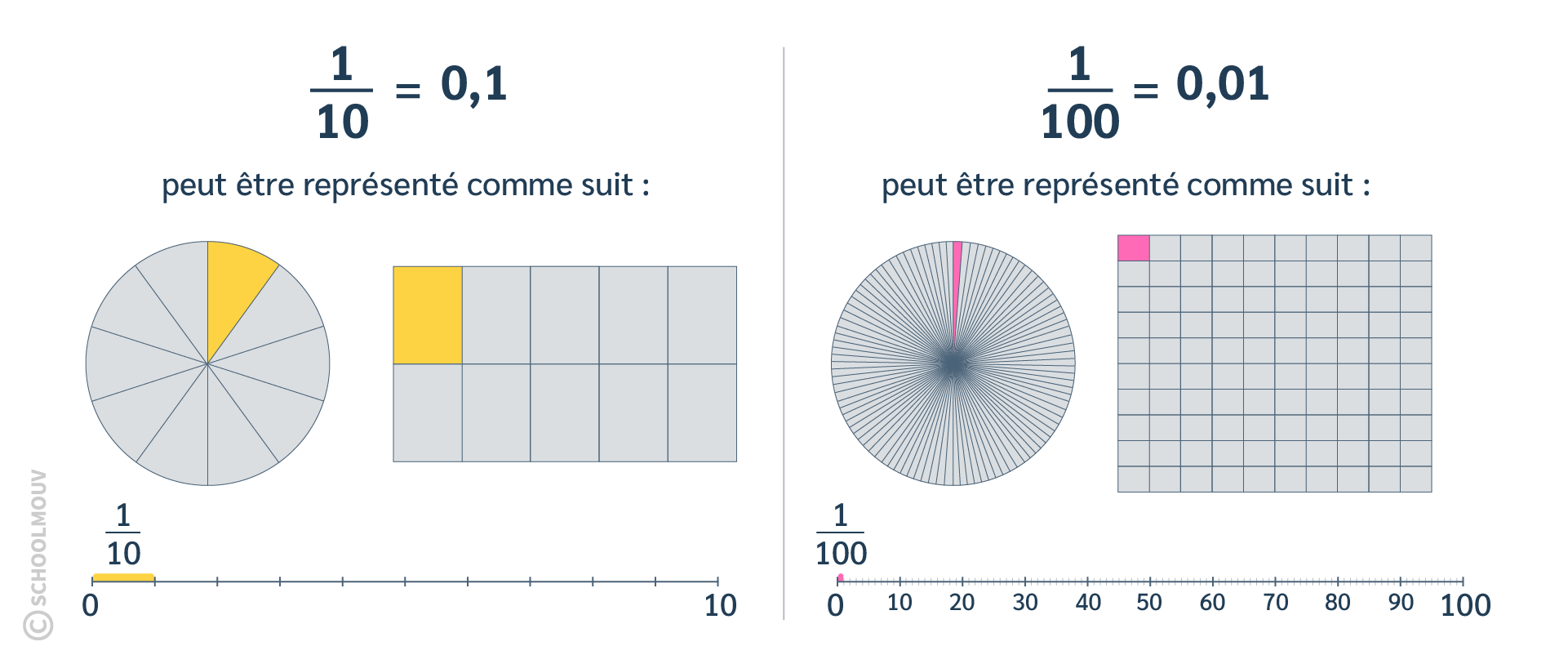
On peut établir des liens également entre les fractions décimales.
Exemples :