Les probabilités

Dans cette leçon, nous allons aborder les probabilités.
Les probabilités, c’est ce qui permet de dire si un événement a plus ou moins de chances d’arriver.

Identifier des expériences aléatoires et leurs issues

À retenir

Une expérience aléatoire, c’est une action liée au hasard et dont on ne peut donc pas prévoir le résultat à l’avance.
Ce que l’on nomme les issues, ce sont tous les résultats possibles de cette expérience.

Prenons des exemples.

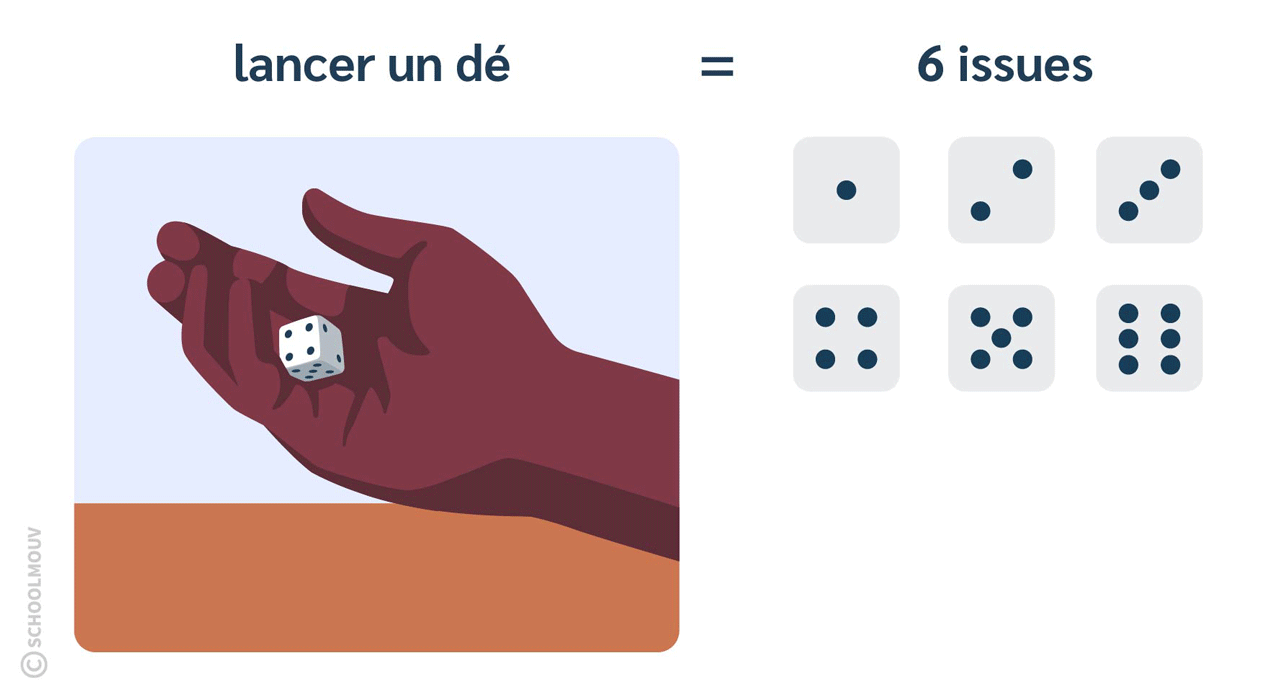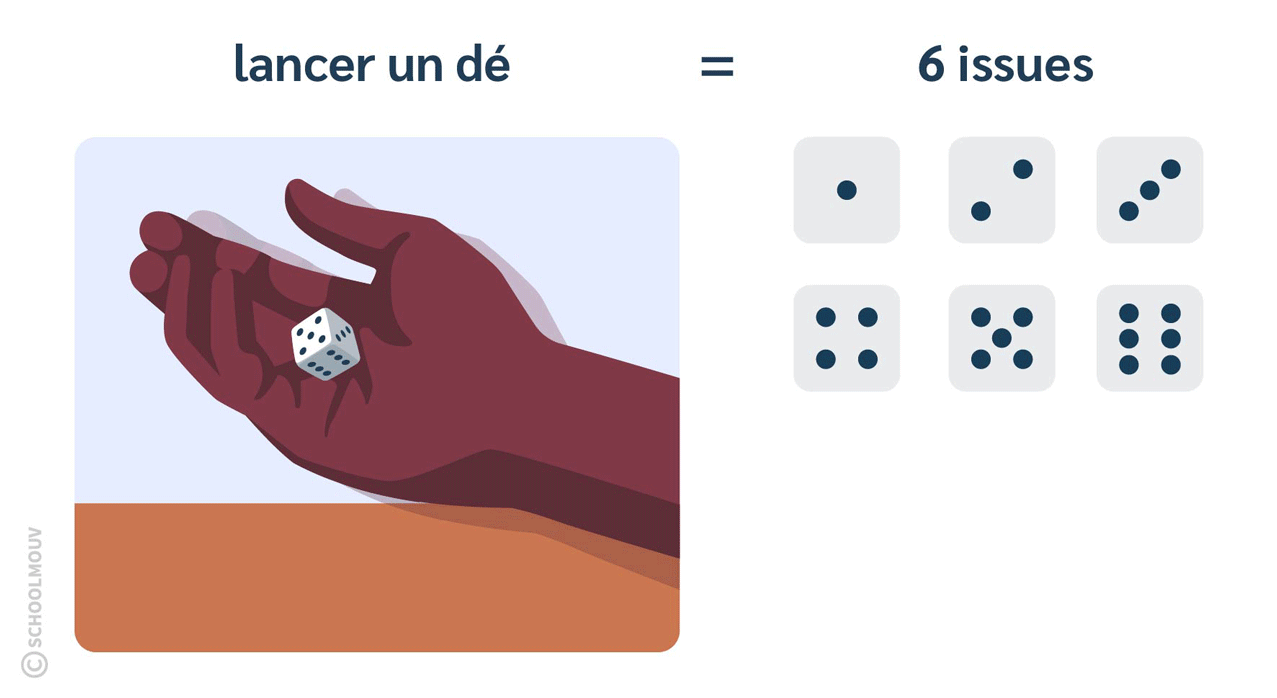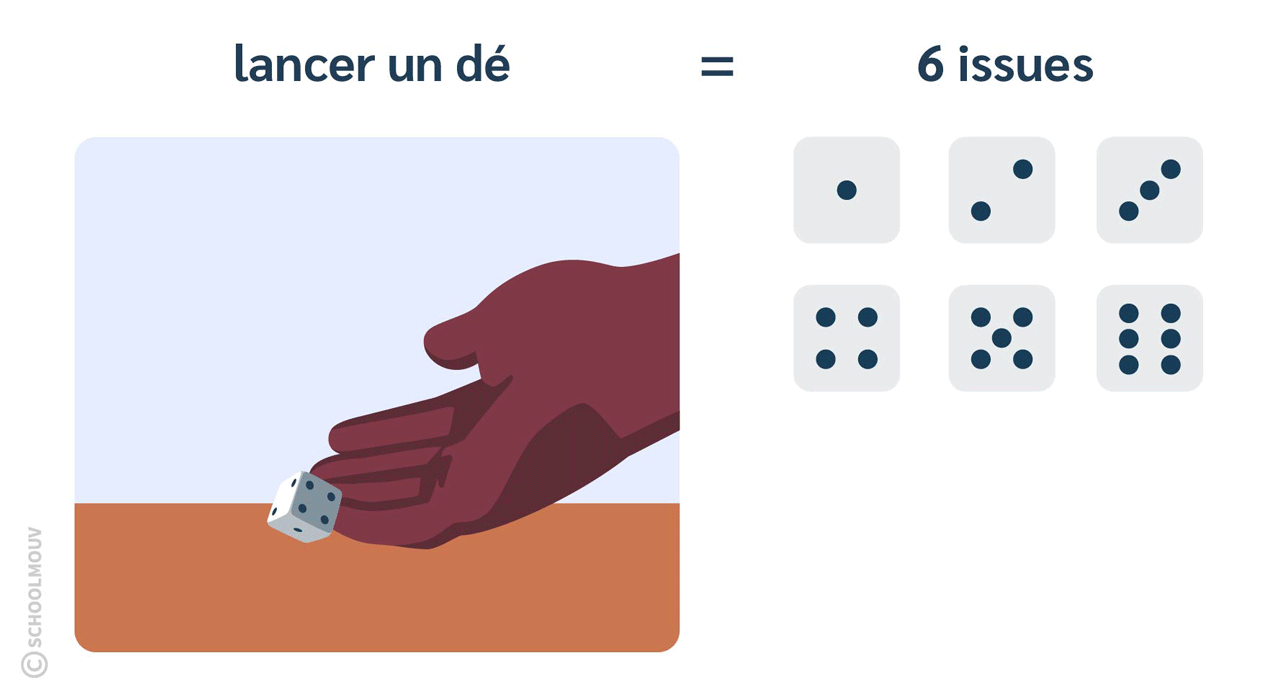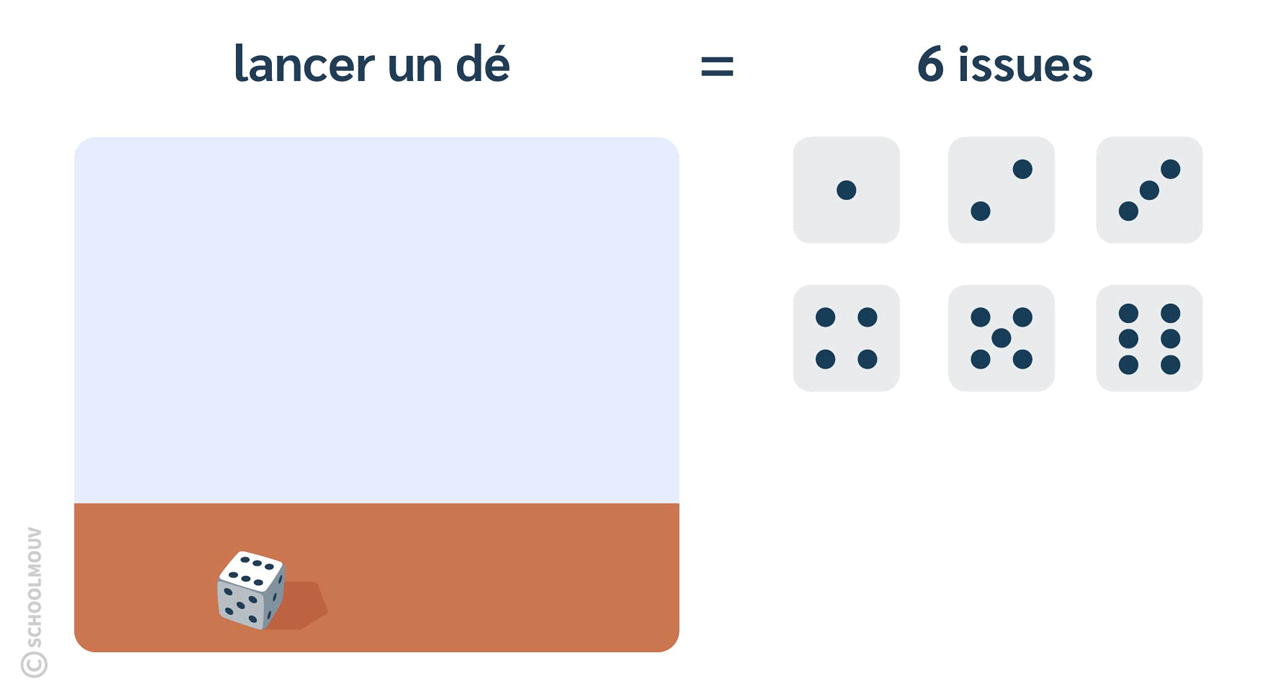
• Lancer un dé est une expérience aléatoire qui a 6 issues.
  En effet, puisque le dé a 6 faces, tu peux tomber sur la face du 1, du 2, du 3, du 4, du 5 ou du 6.

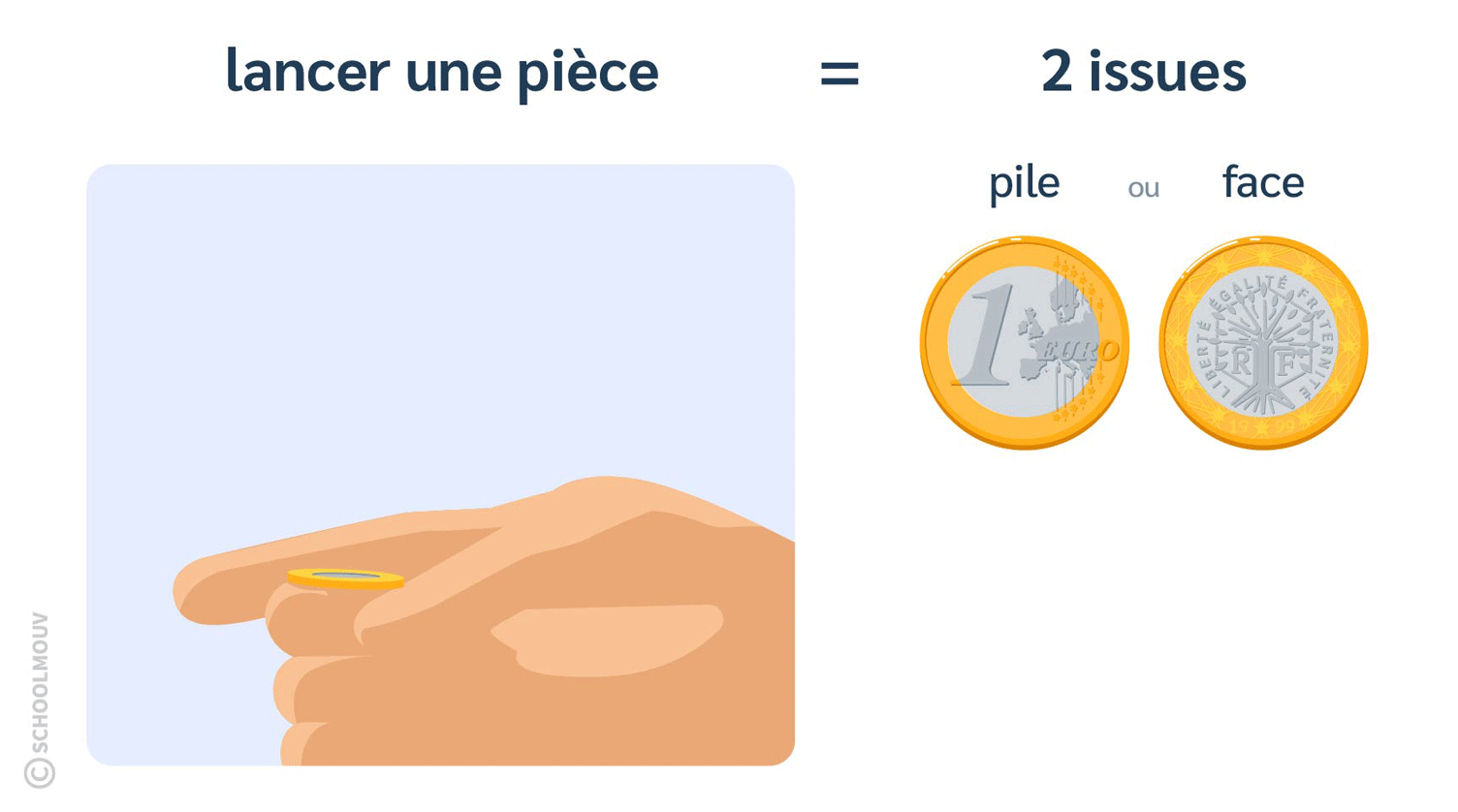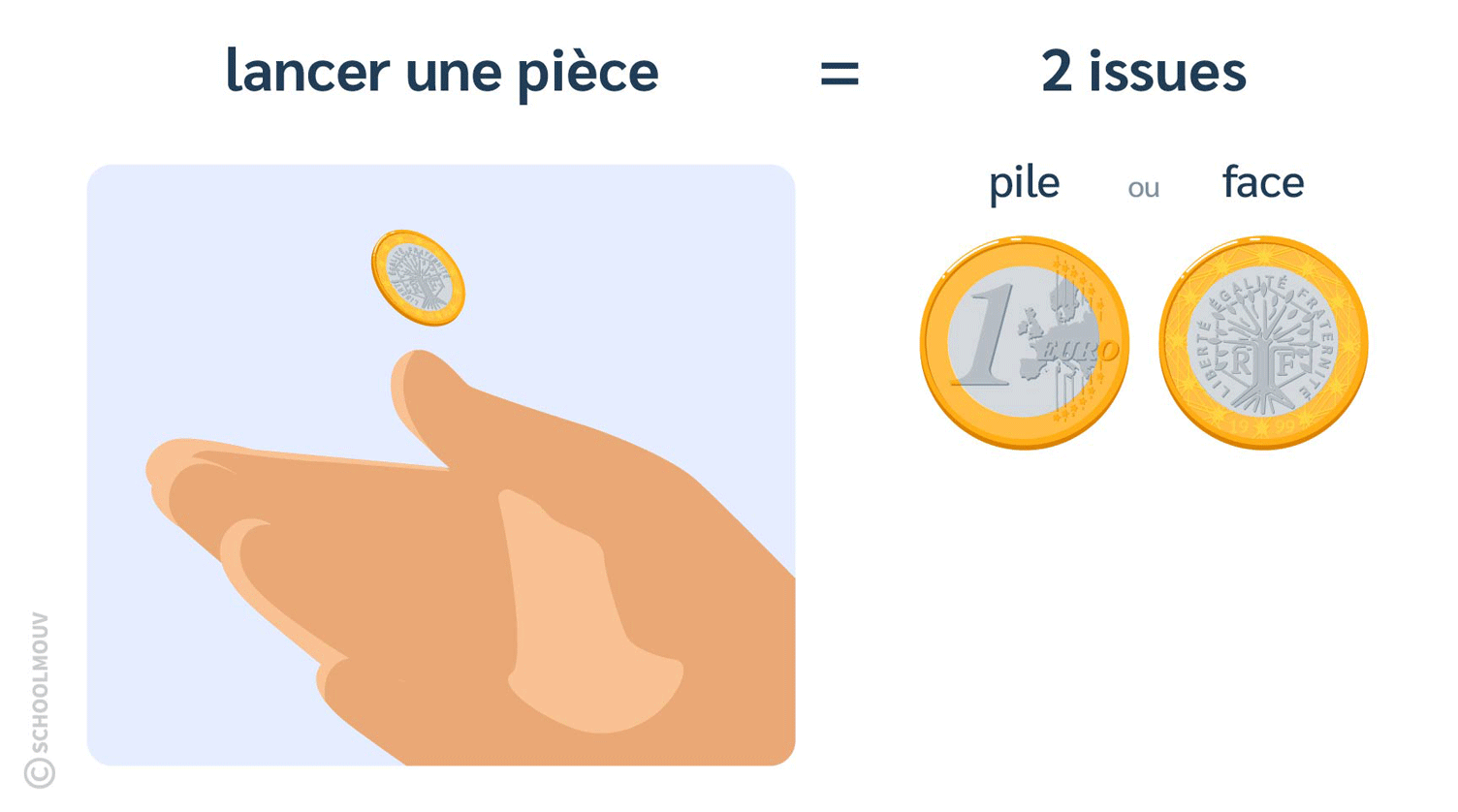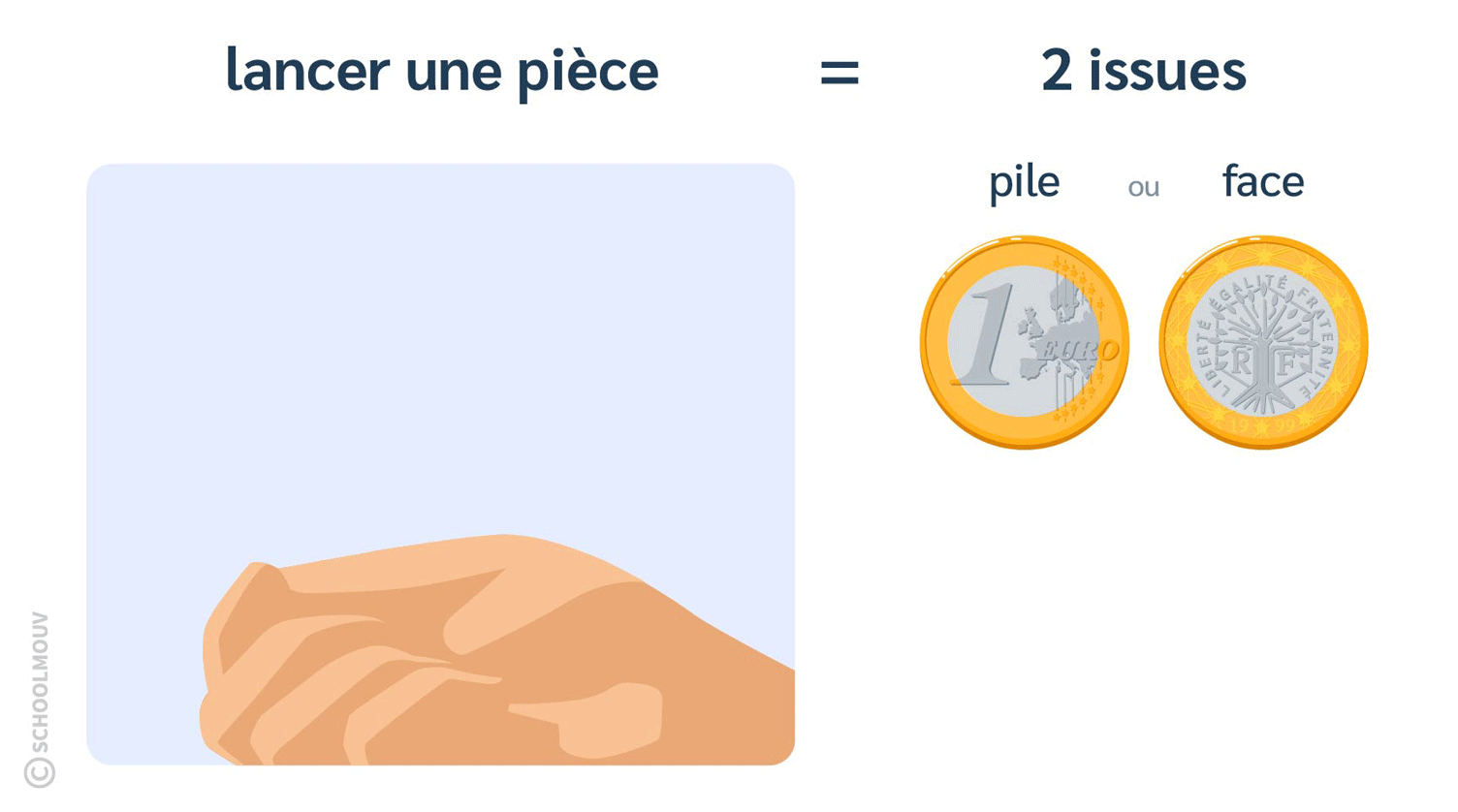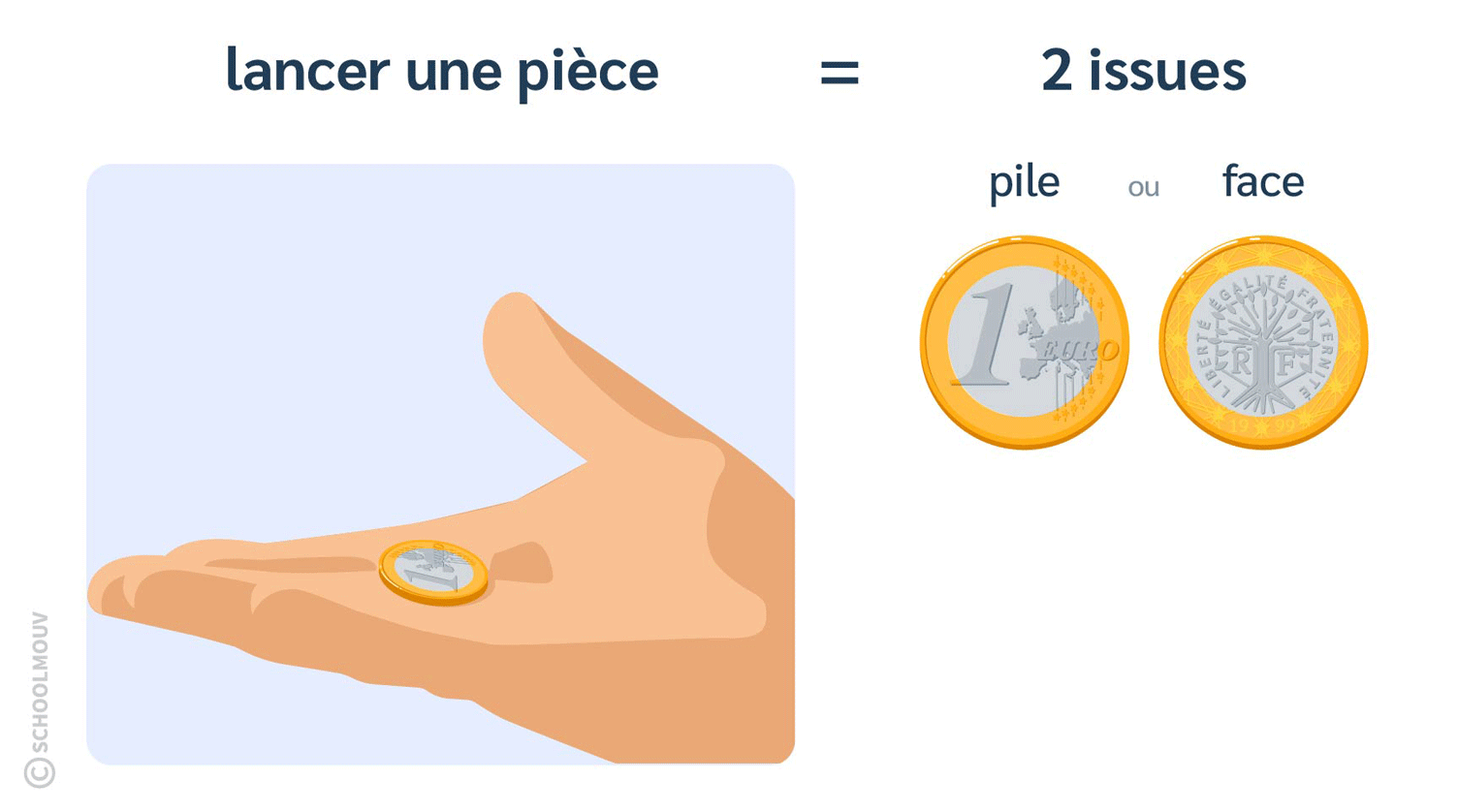
• Lancer une pièce de monnaie est une expérience aléatoire qui a 2 issues.
  En effet, tu peux tomber sur le côté « pile » ou sur le côté « face » de la pièce. Il n’y a pas d’autre possibilité.

• Piocher une carte dans un jeu de 32 cartes est une expérience aléatoire qui a 32 issues.
  Le hasard fait que tu peux piocher n’importe quelle carte parmi les 32 du jeu.

Comparer la probabilité de réalisation d’évènements

À retenir

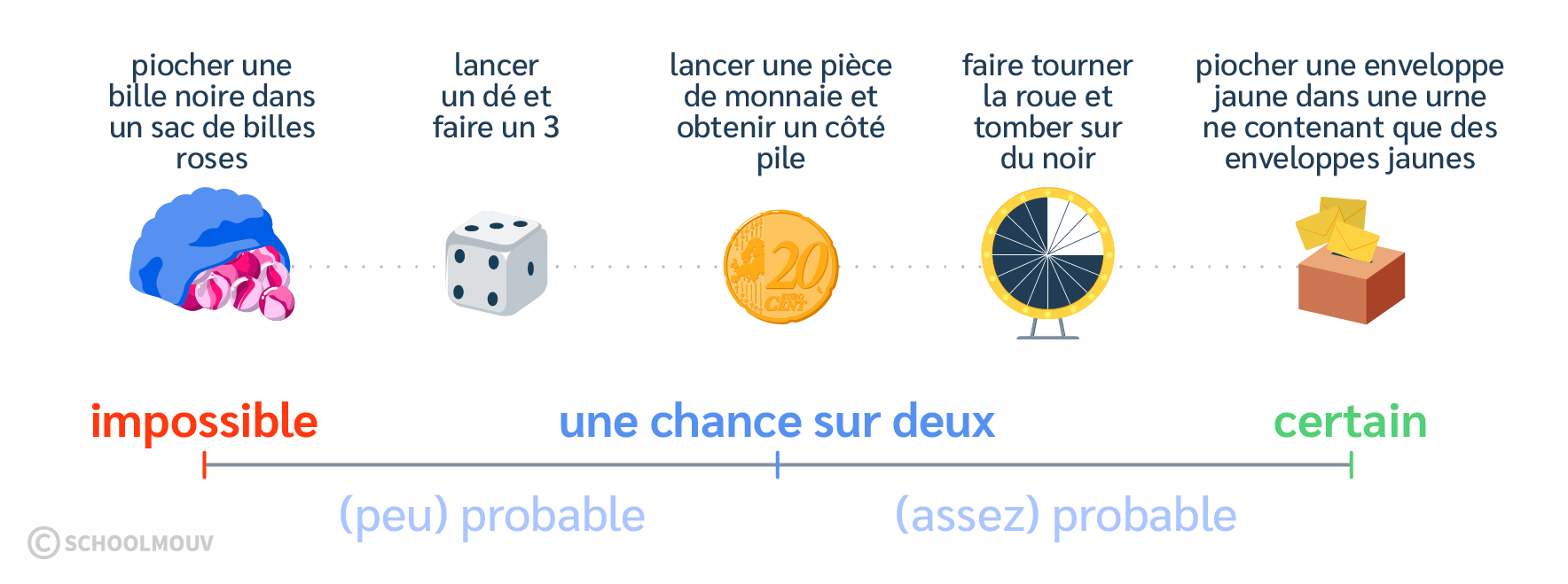
Certains événements sont impossibles. On sait qu’ils n’arriveront jamais.

• ❌ Par exemple, tu ne peux pas obtenir un 7 avec un dé classique.

Certains événements sont certains. On sait, avec certitude, qu’ils arriveront.

• ✅ Par exemple, tu es certain que tu obtiendras un chiffre inférieur à 7, si tu lances un dé classique.

Certains événements sont probables. Ils peuvent arriver mais ce n’est pas certain.

• 🤷 Par exemple, tu peux obtenir un 4 en lançant le dé, mais ce n’est pas sûr.

Attention

Il faut bien différencier un événement « certain » d’un événement « probable ».
Par exemple, je vais voir le maître mardi prochain est un événement très probable. Mais il n’est pas certain à 100 % car un imprévu (ex. : maladie) peut empêcher l’événement de se produire.

Certains événements sont plus probables que d’autres : ils ont plus de chances d’arriver que d’autres.
Par exemple, il est plus probable que tu croises la maîtresse ou le maître un mardi (jour de classe, très probable) plutôt qu’un dimanche (peu probable).

Dans le cas où deux issues possibles ont la même chance de se réaliser, on appelle cela une situation d’équiprobabilité. Les deux issues ont chacune autant de chance que l’autre de se réaliser : on peut parler d’une chance sur deux.
Ainsi, notre exemple précédent sur le lancer d’une pièce de monnaie correspond à une situation d’équiprobabilité : on a une chance sur deux de tomber sur « pile » ou sur « face » ; les deux options ont exactement la même chance de se réaliser.

Parfois, une même expérience a deux résultats possibles, mais cela ne veut pas dire que les deux ont autant de chances d’arriver.

Exemple

Dans un sac, il y a 1 bonbon rouge et 9 bonbons bleus.

On pioche au hasard un seul bonbon.
Il y a bien deux issues possibles : rouge ou bleu.
Mais on a beaucoup plus de chances de tirer un bleu, car il y en a beaucoup plus dans le sac.

De même, si on fait tourner la roue ci-dessous, la flèche peut indiquer deux issues : noir ou blanc.

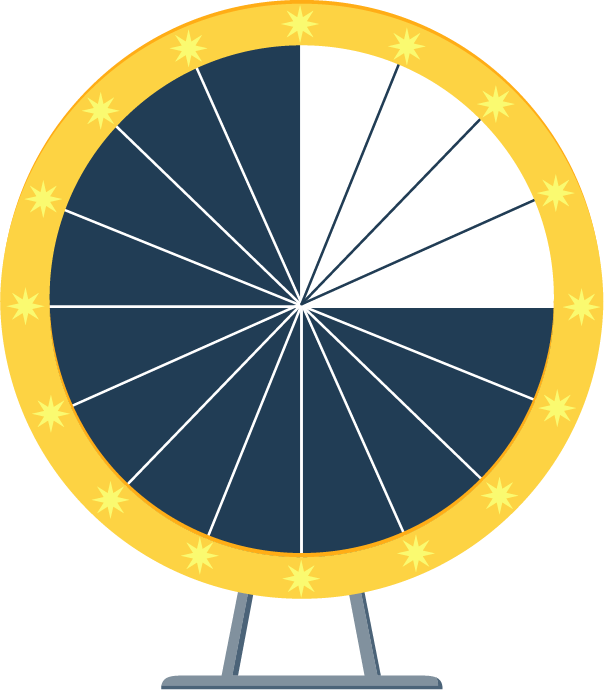
Mais on a beaucoup plus de chances de tomber sur le noir, car il est beaucoup plus présent que le blanc.
L’issue « le résultat est la couleur noire » est la plus probable.

Astuce

On peut organiser des évènements sur cette droite, par ordre de probabilité croissante :

Exemple

Voici comment on pourrait classer certains évènements précis selon leur degré de probabilité :