Résoudre des problèmes avec des produits cartésiens

Produit cartésien de deux ensembles

Pour s’habiller, un enfant a le choix entre :

• 3 shorts : un bleu, un blanc ou un vert ;
• et 5 t-shirts : un jaune, un violet, un orange, un bleu ou un vert.

On peut donc utiliser un tableau à double entrée, puisqu’on a deux ensembles : les shorts et les t-shirts.
Le tableau à double entrée permet de représenter toutes les possibilités qu’a cet enfant pour s’habiller :

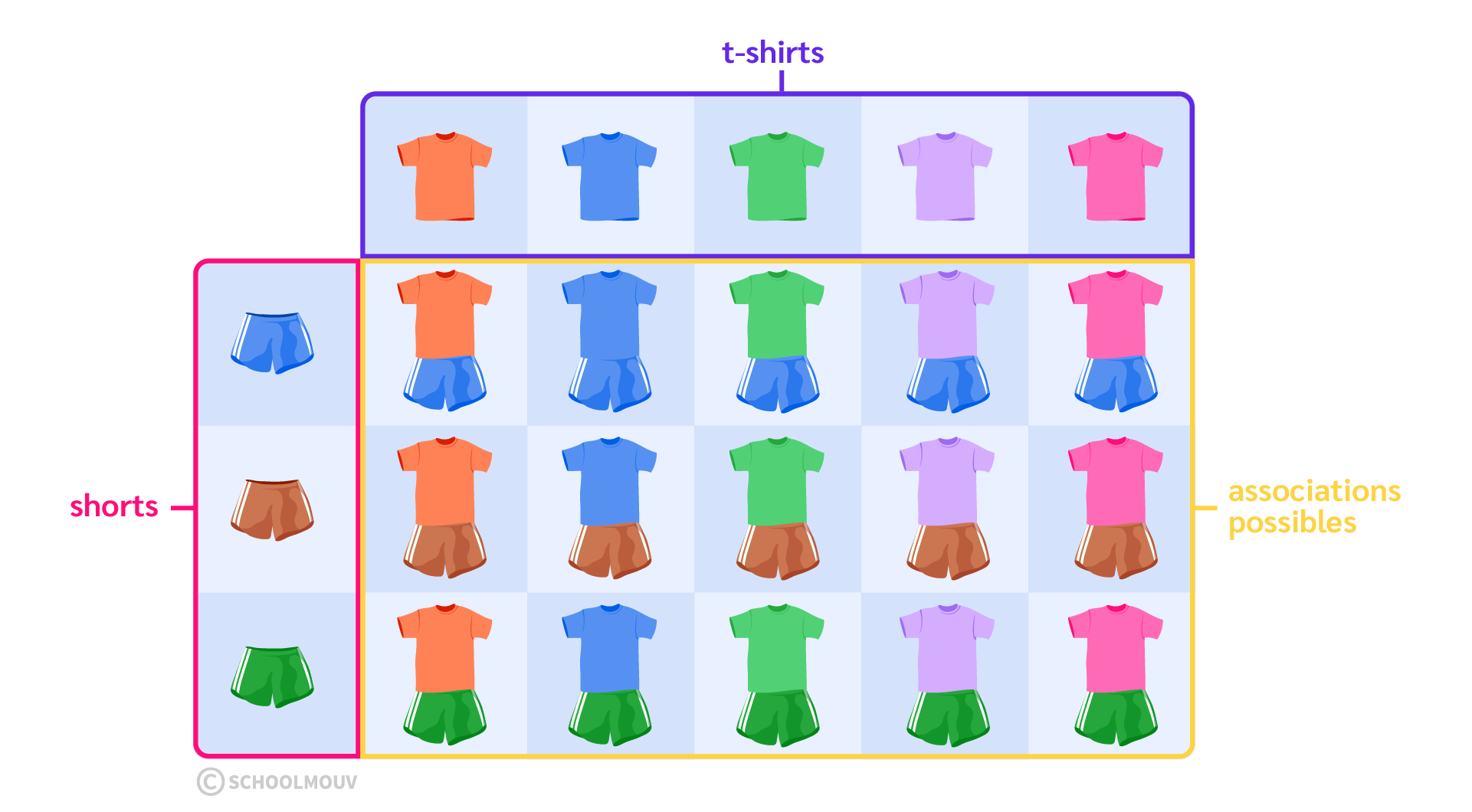
• Si l’on compte le nombre de tenues complètes possibles, il existe 15 options puisque nous avons rempli 15 cases différentes.

Produit cartésien de plus de deux ensembles

Lorsque nous avons 3 ensembles différents, on ne peut plus construire de tableau à double entrée, mais on peut représenter toutes les possibilités sur un arbre.

Prenons l’exemple de papillons : combien de papillons peut-on créer avec 1 corps, 3 paires d’ailes différentes et deux types d’antennes ?

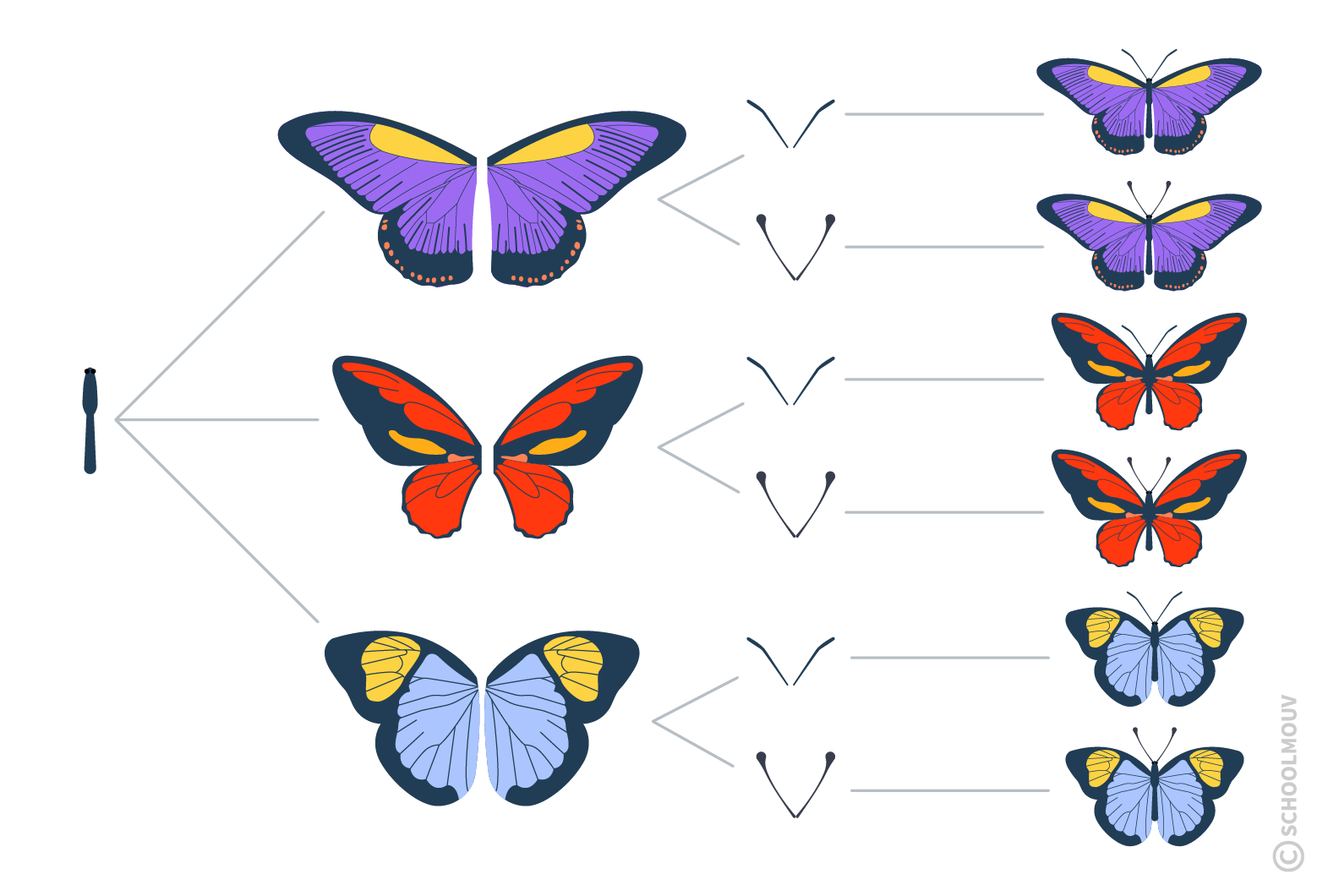
• On peut imaginer que chaque trait représente une branche de l’arbre.
  Grâce à cette représentation, on constate que l’on peut obtenir 6 papillons différents.

Cela fonctionne aussi avec des chiffres, des lettres ou des symboles…

Exemple

Le code pour allumer l’ordinateur commence par la lettre A ou B puis par un chiffre 1, 2 ou 3 puis finit avec le signe ? ou !

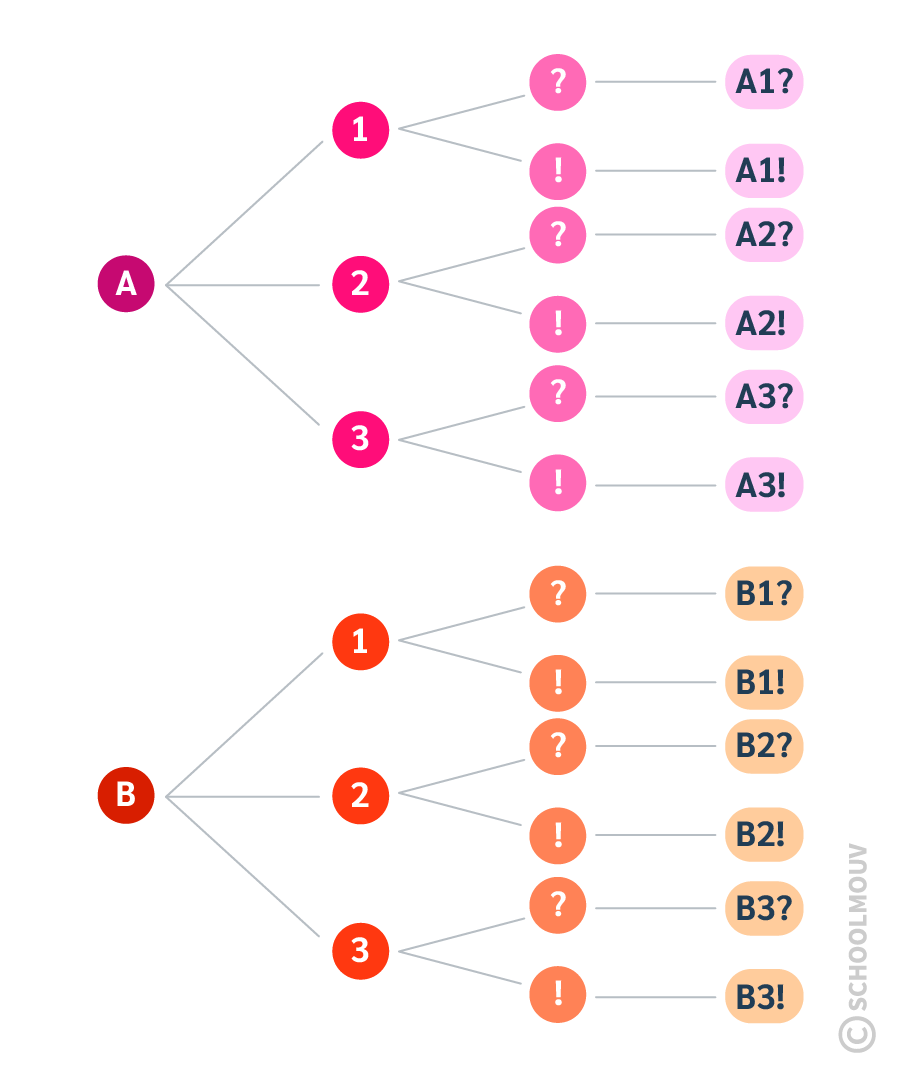
L’arbre permet de lire tous les codes possibles en suivant chaque ligne :

• A1?
• A1!
• A2?
• A2!
• etc.
• En observant l’arbre, on peut compter le nombre de possibilités existantes : ici il y en a 12 au total.