Comparer des fractions

Rappel

Une fraction s’écrit avec une barre de fraction et deux nombres :

• le numérateur est le nombre au-dessus de la barre ;
• le dénominateur est le nombre en-dessous de la barre.

Comparer des fractions ayant le même dénominateur

Lors d’un goûter à l’école, on dispose deux gâteaux sur deux tables.
Les deux gâteaux sont coupés en 8 parts.

Sur l’une des tables, 3 parts ont été mangées. Sur l’autre, 5 parts ont été mangées.
Voici les représentations des deux fractions :

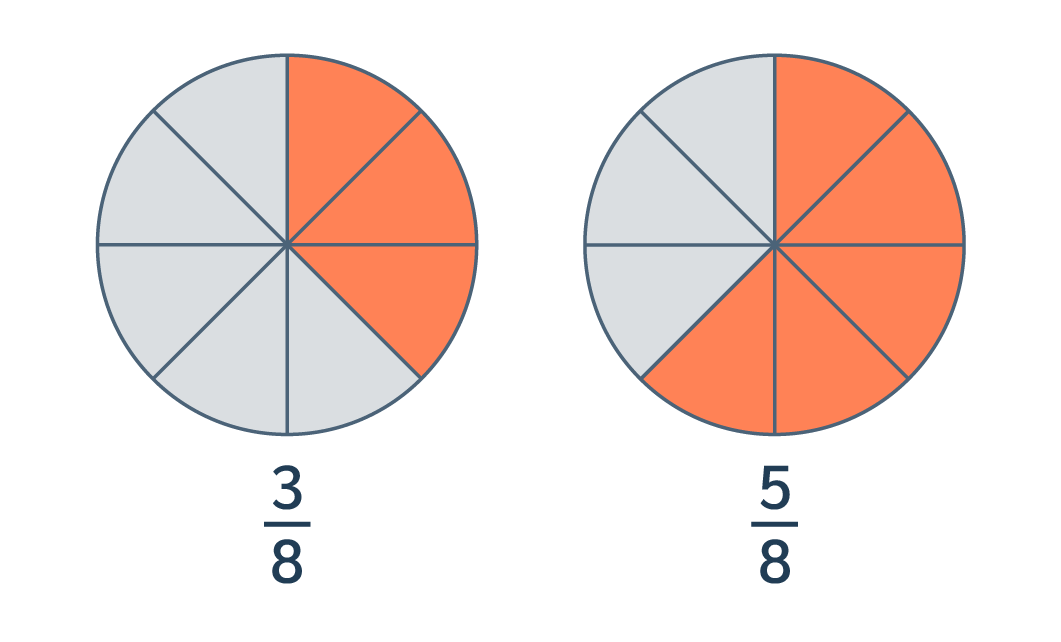
On peut dire que :

• $\dfrac{5}{8}$ est plus grand que $\dfrac{3}{8}$, on écrit : $\dfrac{5}{8}>\dfrac{3}{8}$ ;

OU

• $\dfrac{3}{8}$ est plus petit que $\dfrac{5}{8}$, on écrit : $\dfrac{3}{8}<\dfrac{5}{8}$.

Rappel

Il faut utiliser correctement les signes > (« plus grand que ») et < (« plus petit que »).

À retenir

Lorsque les fractions ont le même dénominateur, il suffit de comparer les numérateurs.
$3<5$, alors $\dfrac{3}{8}<\dfrac{5}{8}$.

Comparer des fractions ayant le même numérateur

Cette fois, on partage deux gâteaux de façons différentes : l’un est coupé en 6 parts, l’autre en 10 parts.

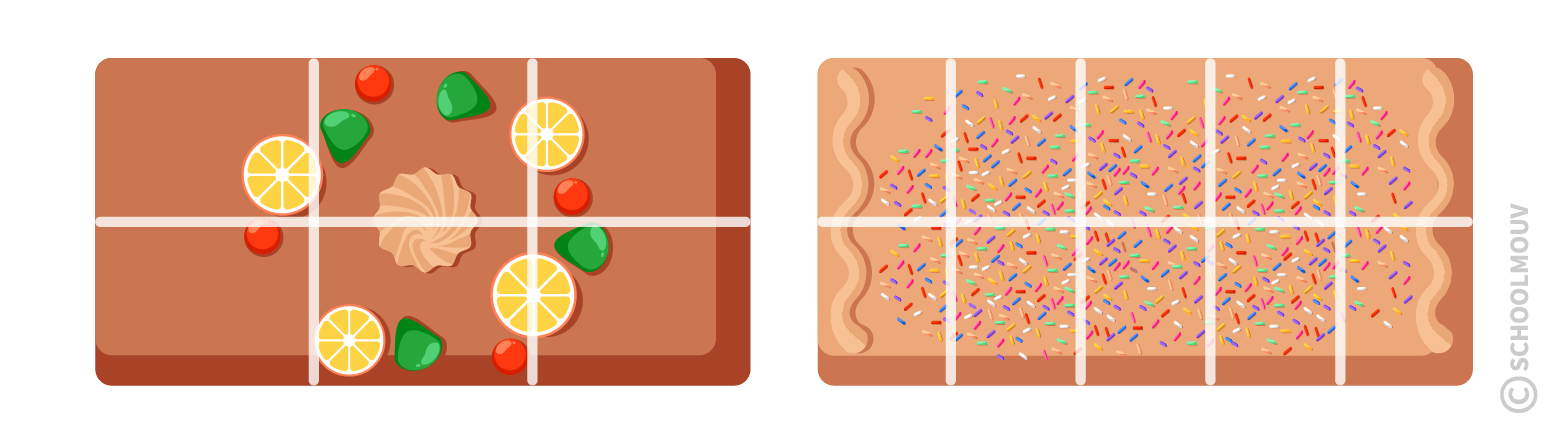
5 parts ont été mangées sur les deux gâteaux.
Voici les représentations des deux fractions :

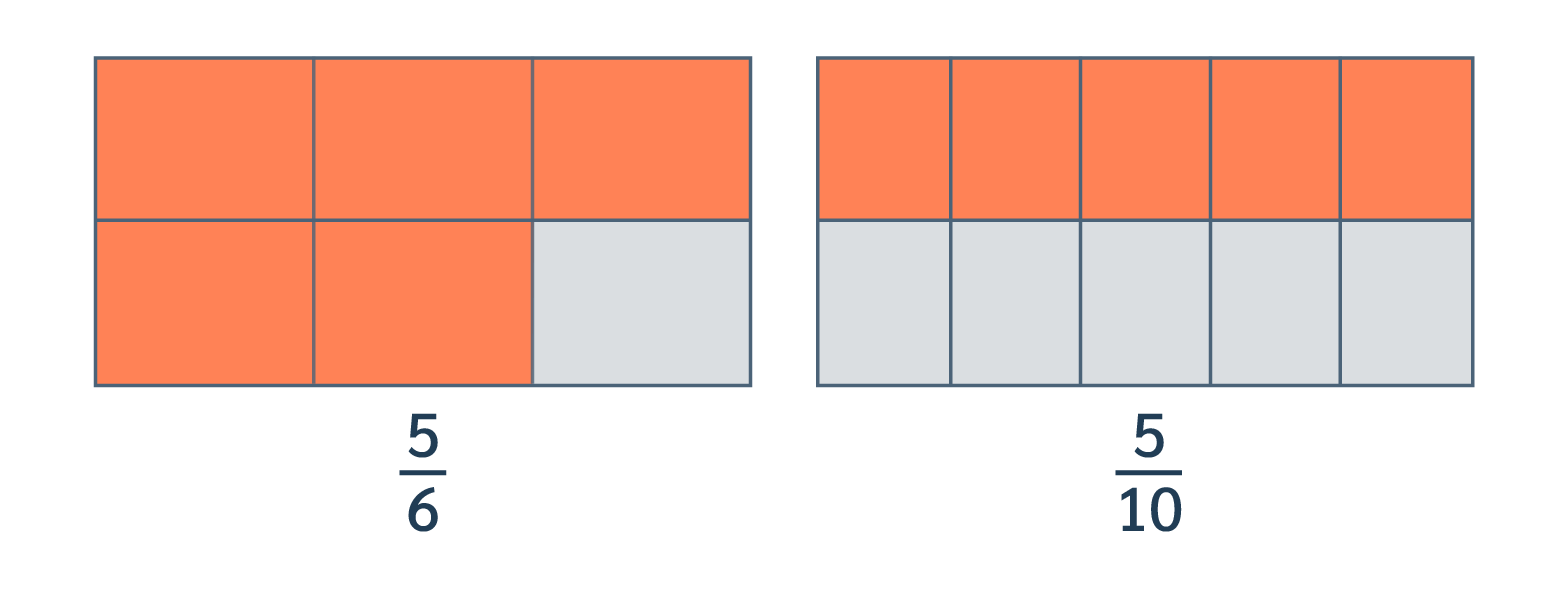
On peut dire que :

• $\dfrac{5}{6}$ est plus grand que $\dfrac{5}{10}$, on écrit : $\dfrac{5}{6}>\dfrac{5}{10}$ ;

OU

• $\dfrac{5}{10}$ est plus petit que $\dfrac{5}{6}$, on écrit : $\dfrac{5}{10}<\dfrac{5}{6}$.

À retenir

Lorsque les fractions ont le même numérateur, on observe les dénominateurs : la fraction qui a le plus grand dénominateur est la plus petite.
$6<10$, alors $\dfrac{5}{6}>\dfrac{5}{10}$. (On remplace < par >.)

Comparer $\dfrac{3}{4}$ et $\dfrac{2}{8}$ par exemple

Il serait plus facile de comparer ces deux fractions si elles avaient le même dénominateur.
Mais ici :

• la première fraction $\dfrac{3}{4}$ a un dénominateur égal à 4 ;
• la deuxième fraction $\dfrac{2}{8}$ a un dénominateur égal à 8.

Cependant, on peut s’aider des égalités des fractions.
En effet, lorsque le dénominateur le plus grand est un multiple de l’autre, on peut comparer les fractions assez facilement.

Astuce

Pour savoir si 8 est un multiple de 4, il faut vérifier si on peut multiplier 4 par un autre nombre pour obtenir 8.

Ici, 8 est bien un multiple de 4, puisque $8=4\times 2$.
Il suffit donc de multiplier par 2 les deux nombres de la fraction $\dfrac{3}{4}$ pour que celle-ci devienne aussi une fraction avec un dénominateur égal à 8.

• On sait ainsi que $\textcolor{#b62921}{\dfrac{3}{4}}$ est égal à $\textcolor{#b62921}{\dfrac{6}{8}}$.

• Comparer $\textcolor{#b62921}{\dfrac{3}{4}}$ et $\dfrac{2}{8}$ revient donc à comparer $\textcolor{#b62921}{\dfrac{6}{8}}$ et $\dfrac{2}{8}$.

Les deux fractions ont alors le même dénominateur : 8.
On peut maintenant comparer les numérateurs :
$6>2$, alors $\textcolor{#b62921}{\dfrac{6}{8}}>\dfrac{2}{8}$.

On a donc la réponse : $\textcolor{#b62921}{\dfrac{3}{4}}>\dfrac{2}{8}$.