Exercices Continuité d'une fonction sur un intervalle

Soit $a$ un réel tel que $a<-0,5$.
Démontrer que $-1<-\dfrac{1}{2a}<1$.

On s’intéresse à la fonction $f$ définie sur $[-4 ; 0[ \cup ]0 ;4]$ par $f(x)=-\dfrac{1}{x}-x-1$ .
Déterminer la dérivée de $f$ et mettre au même dénominateur.

On donne ce tableau de variations :

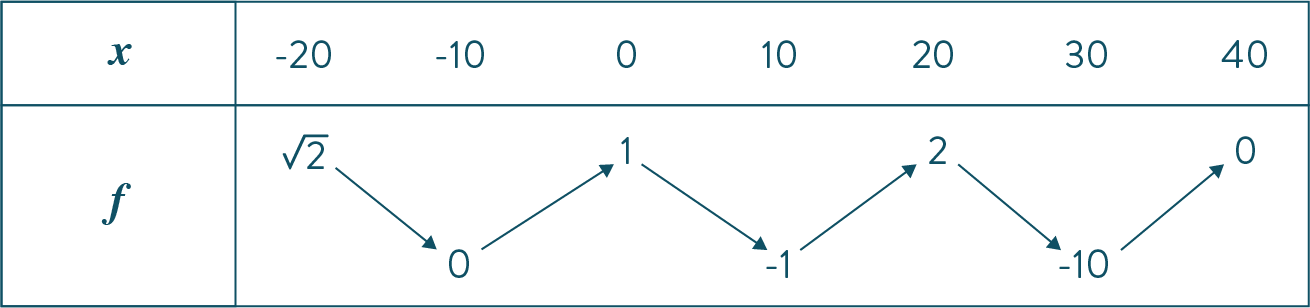
Quel est le nombre de solutions de l'équation $f(x)=1$ ?

On pose $f(x)=\frac{x^3}{x^2+1}$.

Démontrer que $f$ est définie et continue sur $\mathbb{R}$.

Une entreprise fabrique et vend aussitôt $x$ appareils ce mois-ci, 50 € la pièce.
On suppose que $x \in [0 ;100]$.
Les charges dépendent du nombre d’appareils fabriqués, et sont données par la fonction : $$C(x)=0,002x-0,4x+51x+999$$

On demande l’expression des recettes $R(x)$ et du bénéfice $B(x)$.

On pose $f(x)=x^2-x-1$ :

Établir le tableau de variations de $f$ dans $\mathbb{R}$.