Exercices Positions relatives de 2 droites, parralélisme et orthogonilité dans l'espace

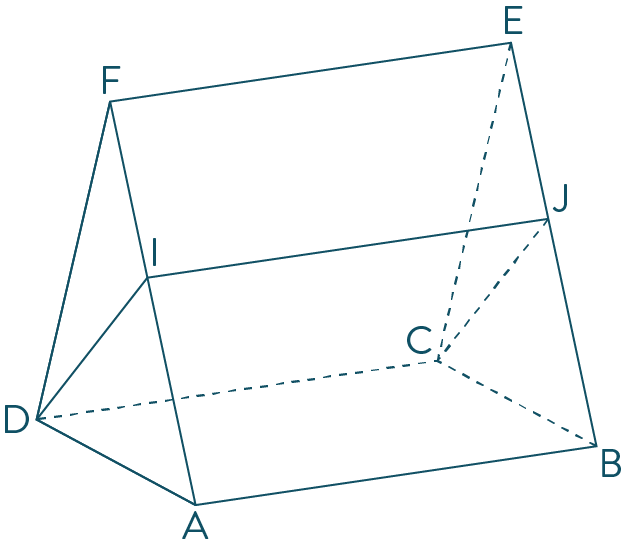
$ABCD$, $AFEB$ et $DFEC$ sont des parallélogrammes, et $(EF)$ parallèle à $(AB)$. La figure $A B D C E F$ est appelée un prisme.
Montrer que $(EF)$ est parallèle à $(CD)$.

Voici une figure représentant un cube de côté $1$ :

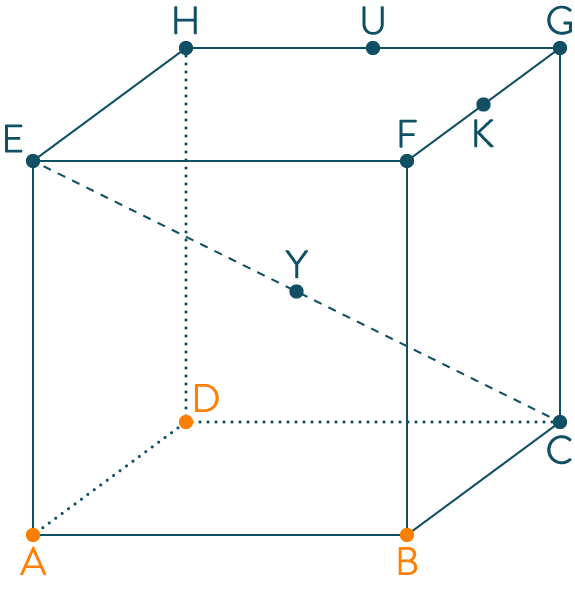
On considère :

• $U$ le milieu de $[HG]$ ;
• $K$ le milieu de $[FG]$ ;
• $Y$ le milieu de $[EC]$.

Parmi les points $Y$, $U$, $K$, $F$, lesquels sont équidistants de $E$ et $C$ ?

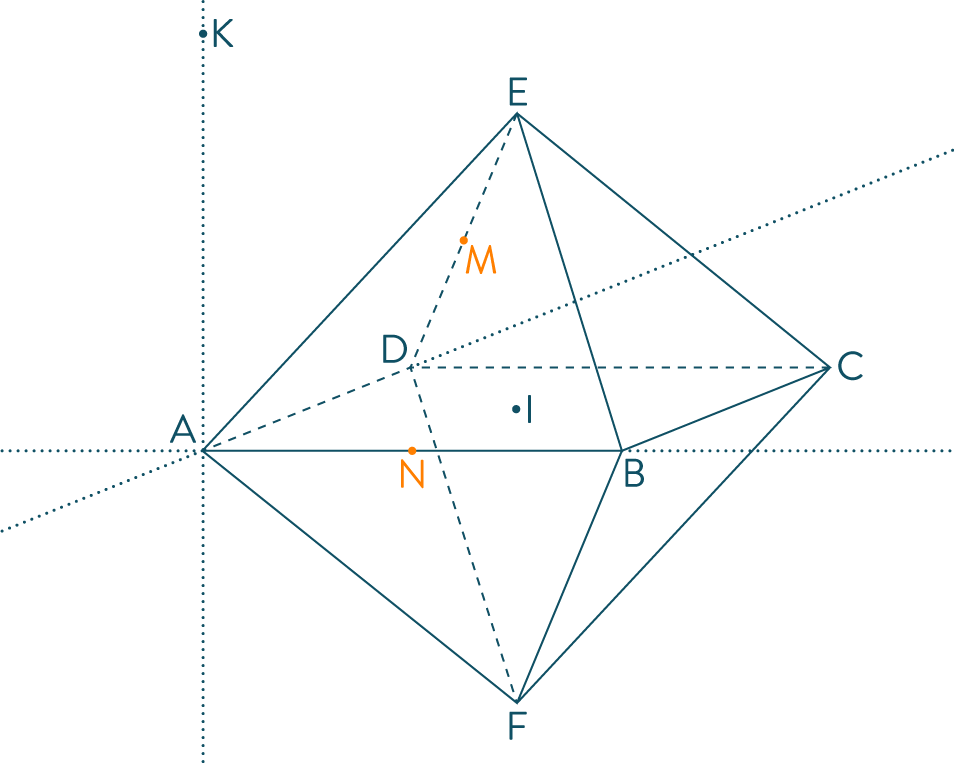
On considère un solide $ADECBF$ constitué de deux pyramides identiques ayant pour base commune le carré $ABCD$ de centre $I$. Toutes les arêtes sont de longueur $1$.
Calculer $AC$.