Exercices Fonction racine carrée et fonction cube

On pose, pour tout réel $x$, $g(x)=x^{3}+x$
On pose aussi $h(x)=x$, $k(x)=x^{2}$, et $l(x)=x^{3}$

Résoudre $g(x)\geq h(x)$

On pose, pour tout réel $x$ : $g(x)=x^{3}$

Démontrer que $g$ est impaire, c’est-à-dire que pour tout réel $x$ on a : $$g(-x)=-g(x)$$

On donne les courbes suivantes :

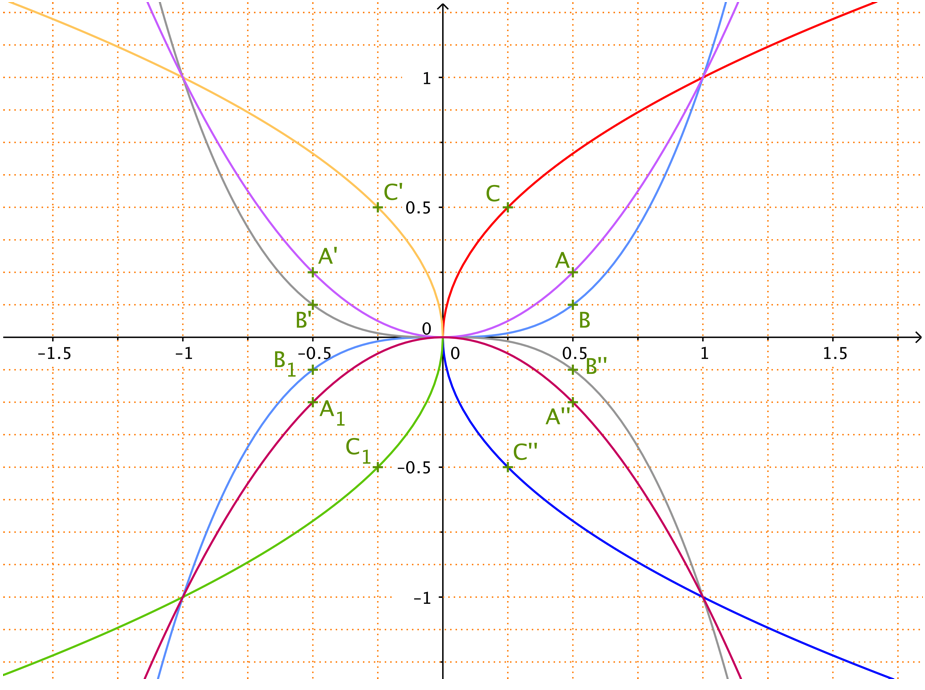
Ces courbes sont toutes celles de fonctions usuelles composées à partir des fonctions $r$ et $c$ définies par :

• $r(x)=\sqrt{x}$ sur $[0;+\infty[$
• $f(x)=x^{2}$ sur $\mathbb{R}$
• $c(x)=x^{3}$ sur $\mathbb{R}$

Déterminer une fonction possible dont la courbe contienne le point $A$.
Cette courbe contient-elle un autre point de la figure ?