Exercices Calcul Intégral : intégration d'une fonction

Calculer la valeur moyenne $m$ sur $[0;\pi]$ de la fonction $f$ définie par $f(x)=sin \, x$.

Soit $f$ définie sur $\mathbb{R}$ par $f(x)=x$.
On demande la valeur moyenne de $f$ sur $[0,1]$.

On considère la fonction $f$ donnée par sa courbe :

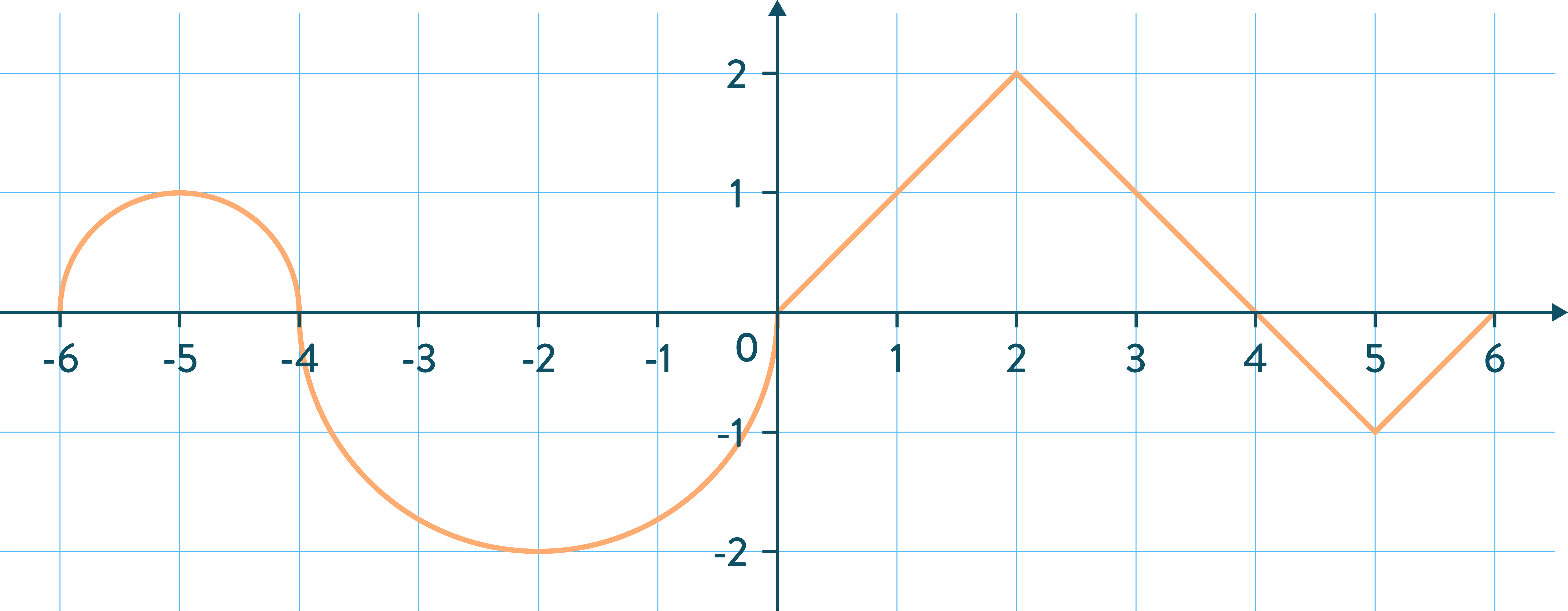
Donner le signe de $\int^{-4}_{-6}f(x)d(x)$ et celui de $\int^0_{-4}f(x)d(x)$.

On définit la fonction $f$ par morceaux :

$f(x)= \left\lbrace \begin{array}{ccc} \dfrac{-1}{x^2} & \text{si} \, & 1\leqslant x < \dfrac{\pi}{2} \\ \dfrac{x \cos x-\sin x}{x^2} & \text{si} \, & \dfrac{\pi}{2} \leqslant x < \pi \\ -\dfrac1x + 2\cos x \sin x & \text{si} \, & {\pi} \leqslant x \leqslant 2\pi\end{array}\right.$

Peux-ton affirmer que la fonction $f$ est continue sur $[1;3\pi]$ ?

Une entreprise vend des peluches et s’intéresse à la quantité vendue, jour après jour, au cours de l’année 2017. Elle s’aperçoit que les ventes ont suivi la courbe suivante :

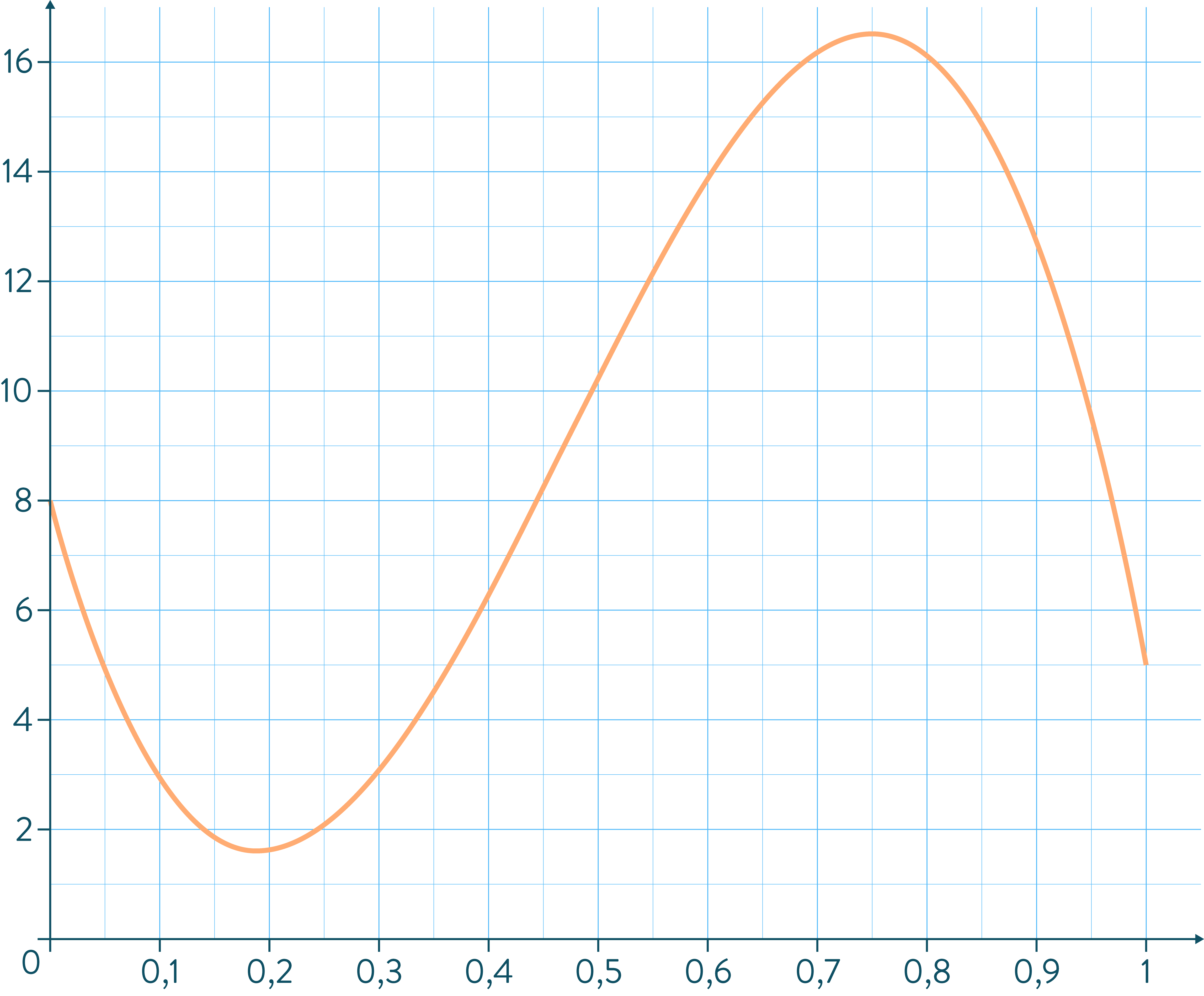
L’abscisse $0$ correspond au 1^er janvier, l’abscisse $1$ au 31 décembre de l’année 2017 (qui compte 365 jours).

Ainsi, si les jours sont numérotés de 0 à 364 (qui correspondent aux jours du 1^er janvier jusqu’au 31 décembre), le jour numéro $n$ correspond à l’abscisse $\dfrac{n}{364}$.

Par exemple, le 20 janvier 2017 c’est le jour numéro 19 donc l’abscisse $\dfrac{19}{364}\approx 0,05$ (à 0,05 près) soit une ordonnée de 5. Le graphique nous indique que le 20 janvier, l’entreprise a vendu 5 peluches.
Combien l’entreprise a-t-elle vendu de peluches (on arrondira à l’unité) au jour $n_{326}$ et à quel jour de l’année cela correspond-t-il ?

Pour cette question, on utilisera une calculatrice.