
01 86 76 13 95
(Appel gratuit)
On donne quatre points :
Démontrer que $ABCD$ n’est pas un parallélogramme.
On donne quatre points $A$, $B$, $C$ et $D$ quelconques.
Soit $G$ le milieu de $[AB]$, démontrer que $\overrightarrow{GA}=\frac{1}{2}\overrightarrow{BA}$
Dans un repère $(O,\vec{u},\vec{v})$, on considère $A(1;1)$, $I(0;1)$, $J(0;1)$, $C(0;3)$ et $D(x;0)$ où $x$ est inconnu.
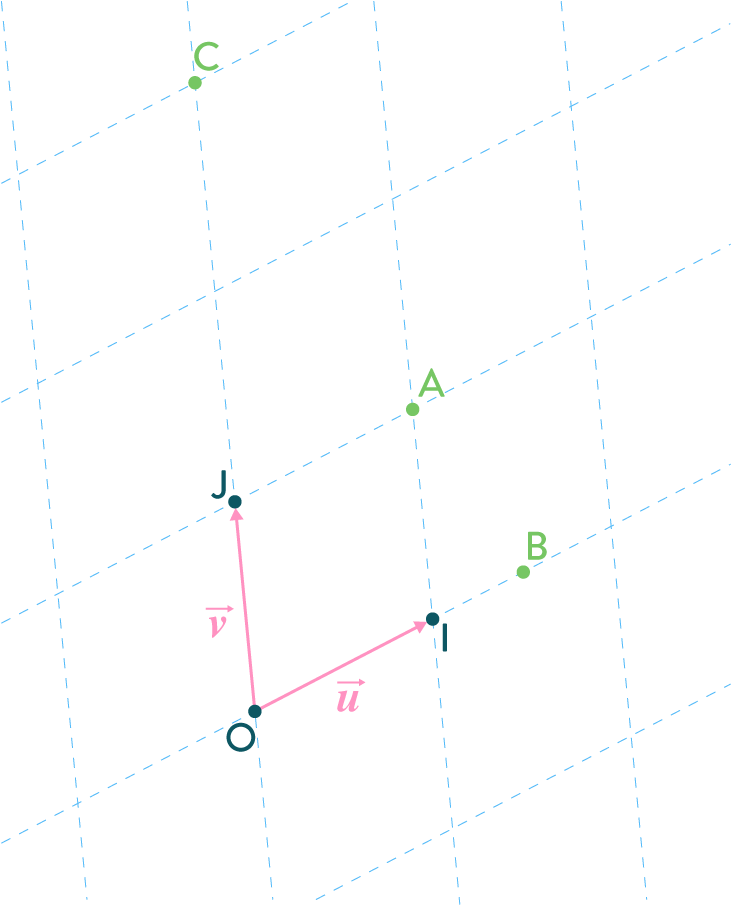
Déterminer les coordonnées du vecteur $\overrightarrow{CA}$.