Exercices Repère et coordonnées de vecteurs

Dans un repère orthonormé $(O,\vec{i},\vec{j})$, on donne les points suivants :

• $A(-2;1)$
• $B(-1;-1)$
• $C(1;0)$
• $D(3;1)$

Démontrer que $ABC$ est isocèle en $B$.

On donne quatre points :

• $A(-2;-1)$
• $B(-3;-5)$
• $C(0;-2)$
• $D(1;3)$

Démontrer que $ABCD$ n’est pas un parallélogramme.

Dans un repère orthonormé $(O,\vec{i},\vec{j})$, on donne les points suivants :

• $A(-1;-2)$
• $B(-2;-4)$
• $C(0;-4)$
• $D(-1;-6)$

Calculer les coordonnées du milieu $I$ de $[AD]$.

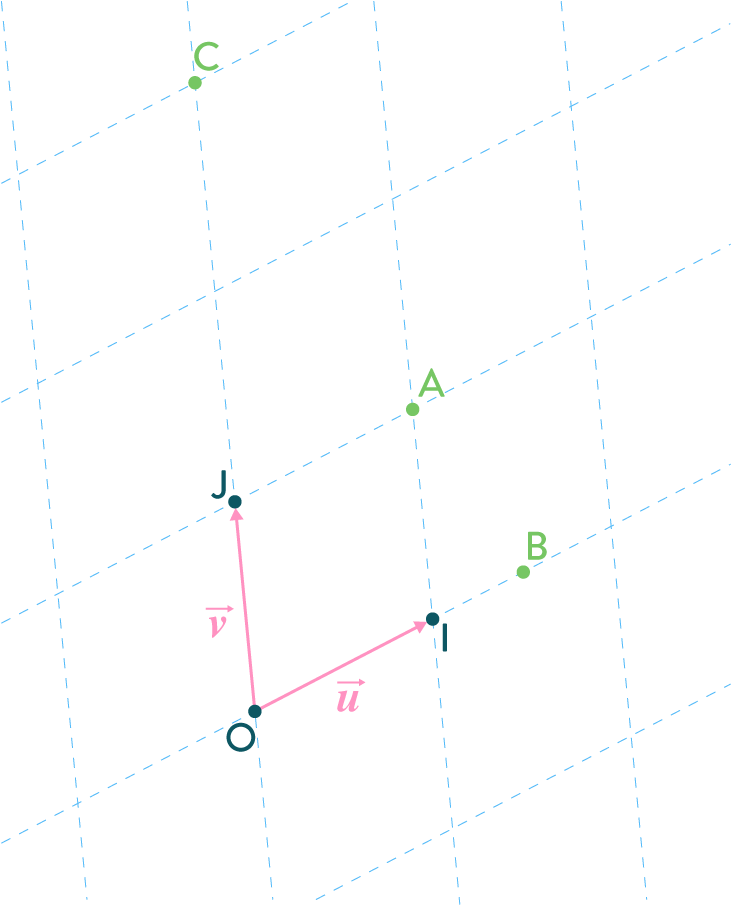
Dans un repère $(O,\vec{u},\vec{v})$, on considère $A(1;1)$, $I(1;0)$, $J(0;1)$, $C(0;3)$ et $D(x;0)$ où $x$ est inconnu.

Déterminer les coordonnées du vecteur $\overrightarrow{CA}$.