Déjà plus de
1 million
d'inscrits !
N°1
pour apprendre & réviser du collège au lycée.
Comprendre et utiliser des nombres entiers pour ordonner et comparer des nombres entiers inférieurs à 1 000
Prérequis :
- Comprendre et utiliser des nombres entiers pour ordonner et comparer des nombres entiers inférieurs à 20,
- Comprendre et utiliser des nombres entiers pour ordonner et comparer des nombres entiers inférieurs à 100.
Pourquoi apprendre à comparer et à ranger les nombres entiers inférieurs à 1 000 ?
- Pour savoir qui en a le plus, qui en a le moins.
- Pour comparer des prix (le plus cher, le moins cher), des distances (le plus loin, le moins loin), etc.
- Pour savoir ranger des nombres du plus petit au plus grand et inversement.
Rappel
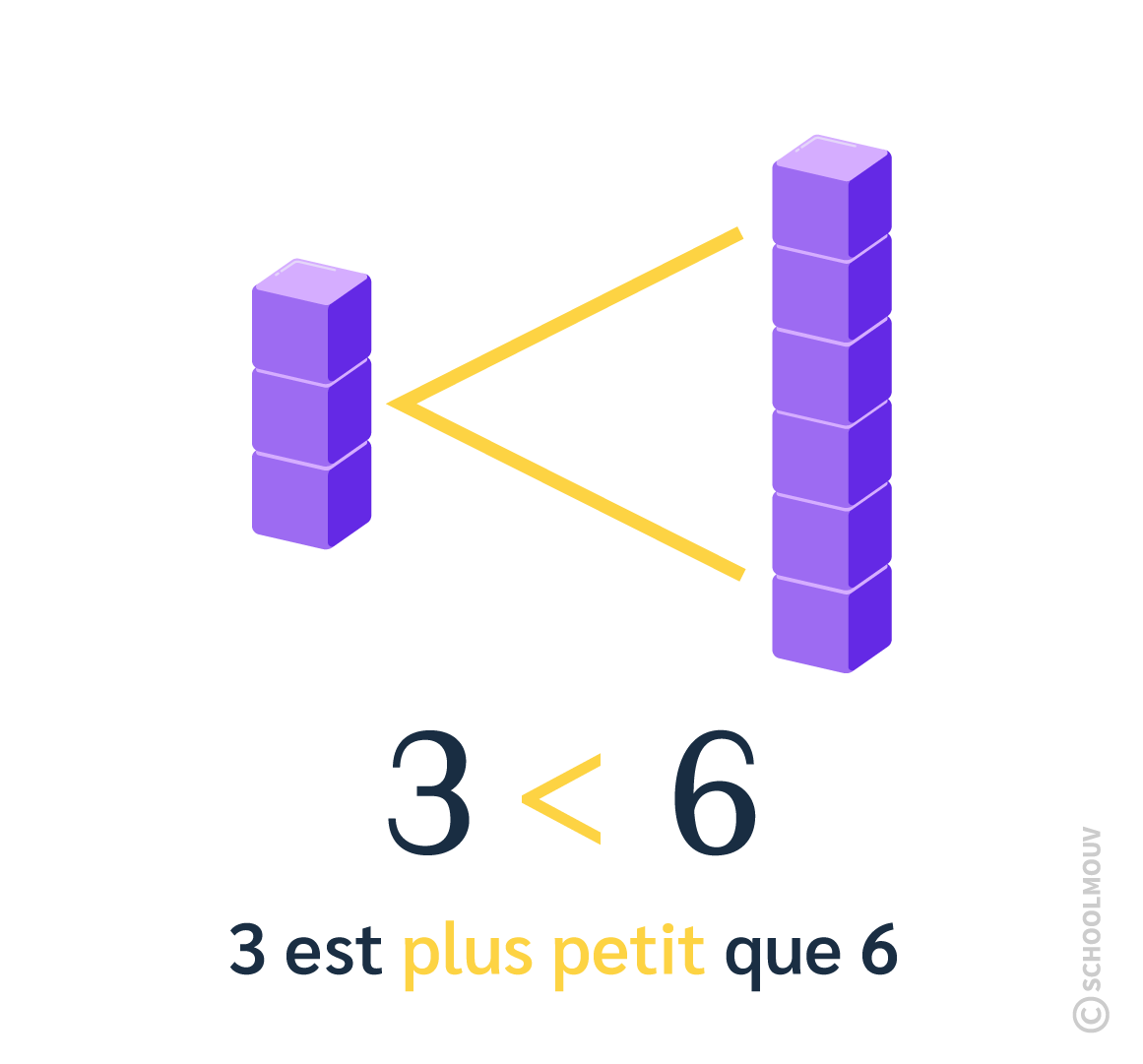
Pour comparer et ranger les nombres, on utilise les signes < et >.
Quand 2 nombres sont égaux, on utilise le signe =.
Comparer des nombres
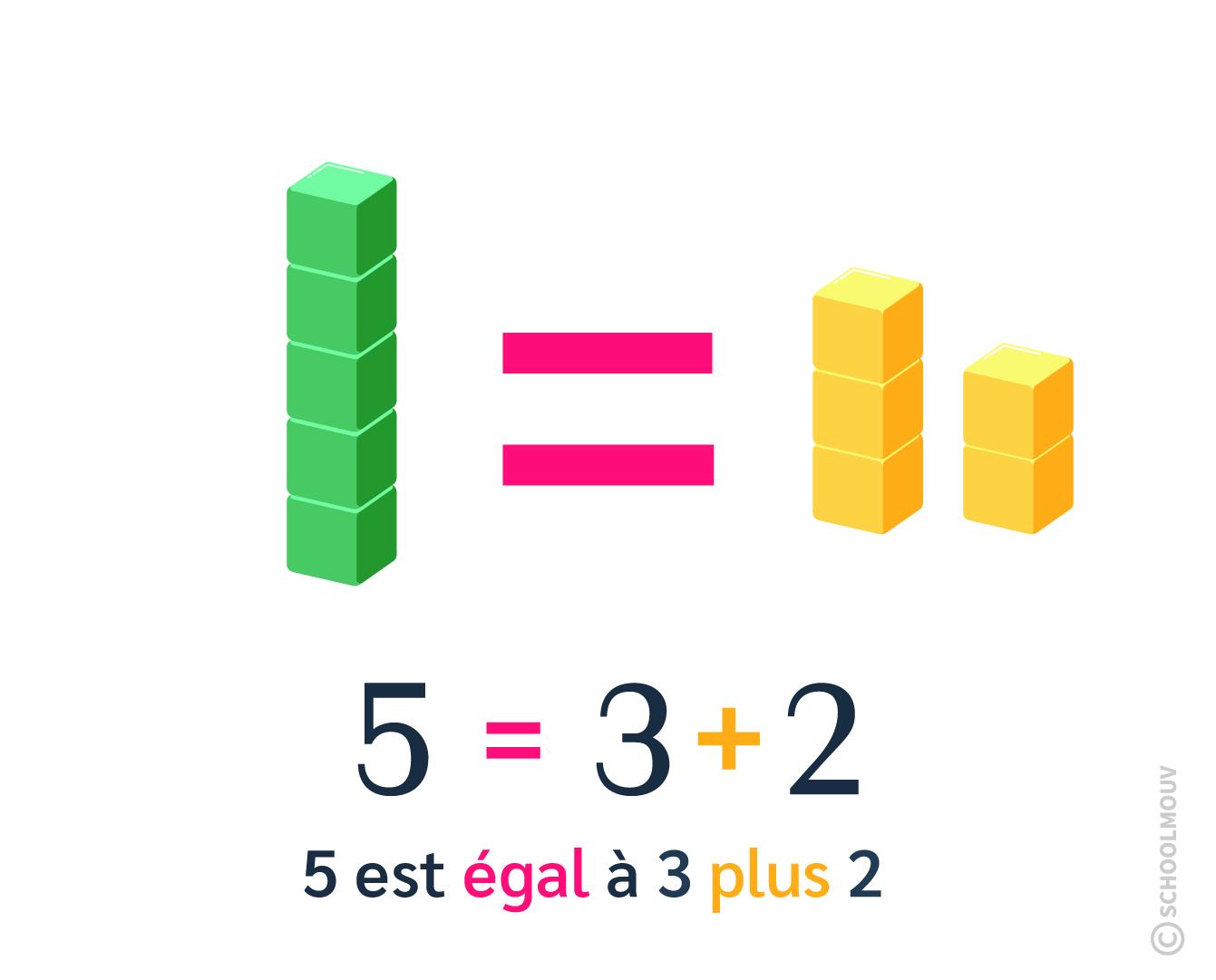
Comparer des nombres
Pour comparer des nombres inférieurs à 1 000 :
- on commence par comparer les chiffres des centaines ;
Exemple
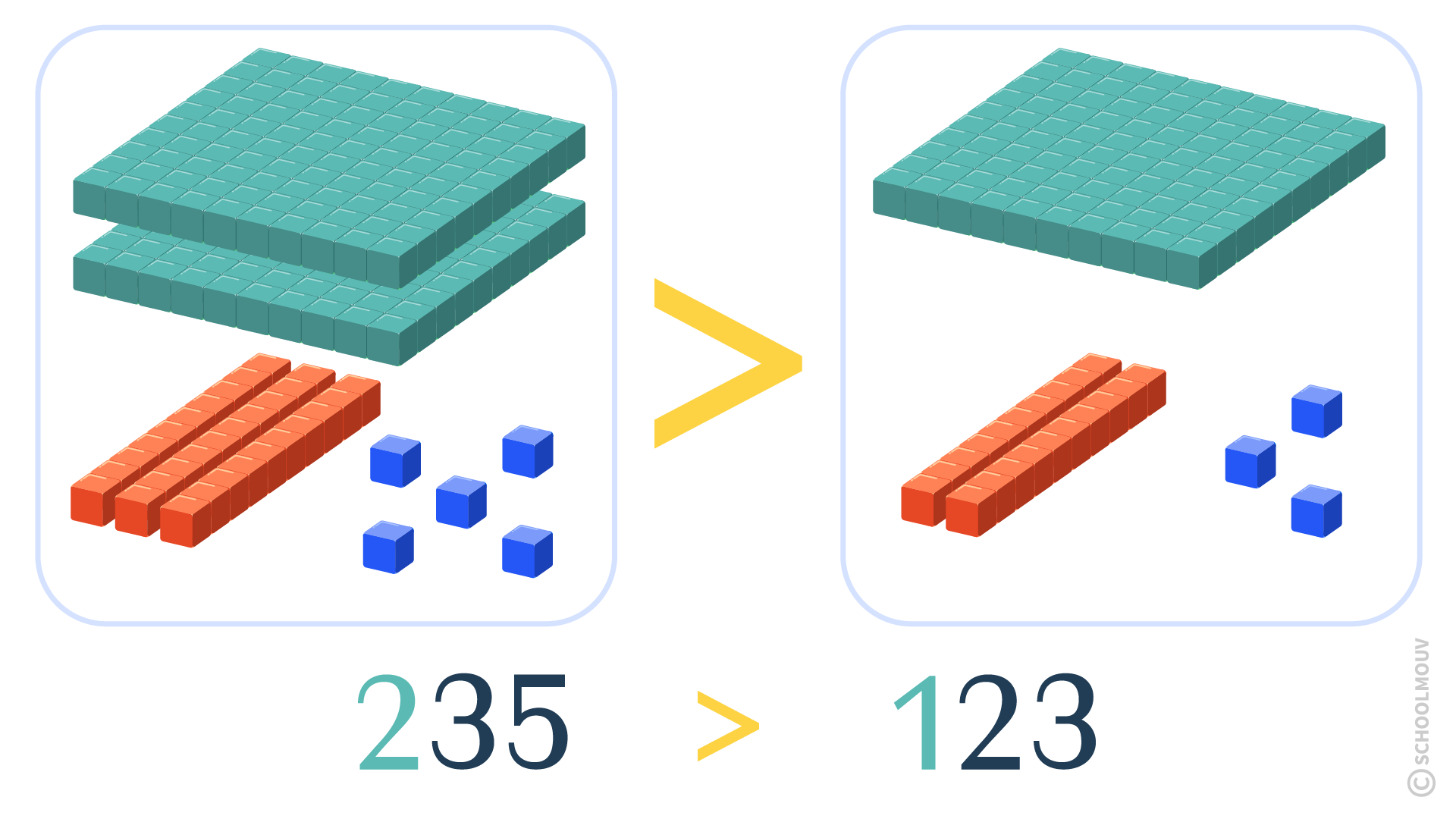
- 235 est plus grand que 123.
- si les chiffres des centaines sont identiques, on compare les chiffres des dizaines ;
Exemple
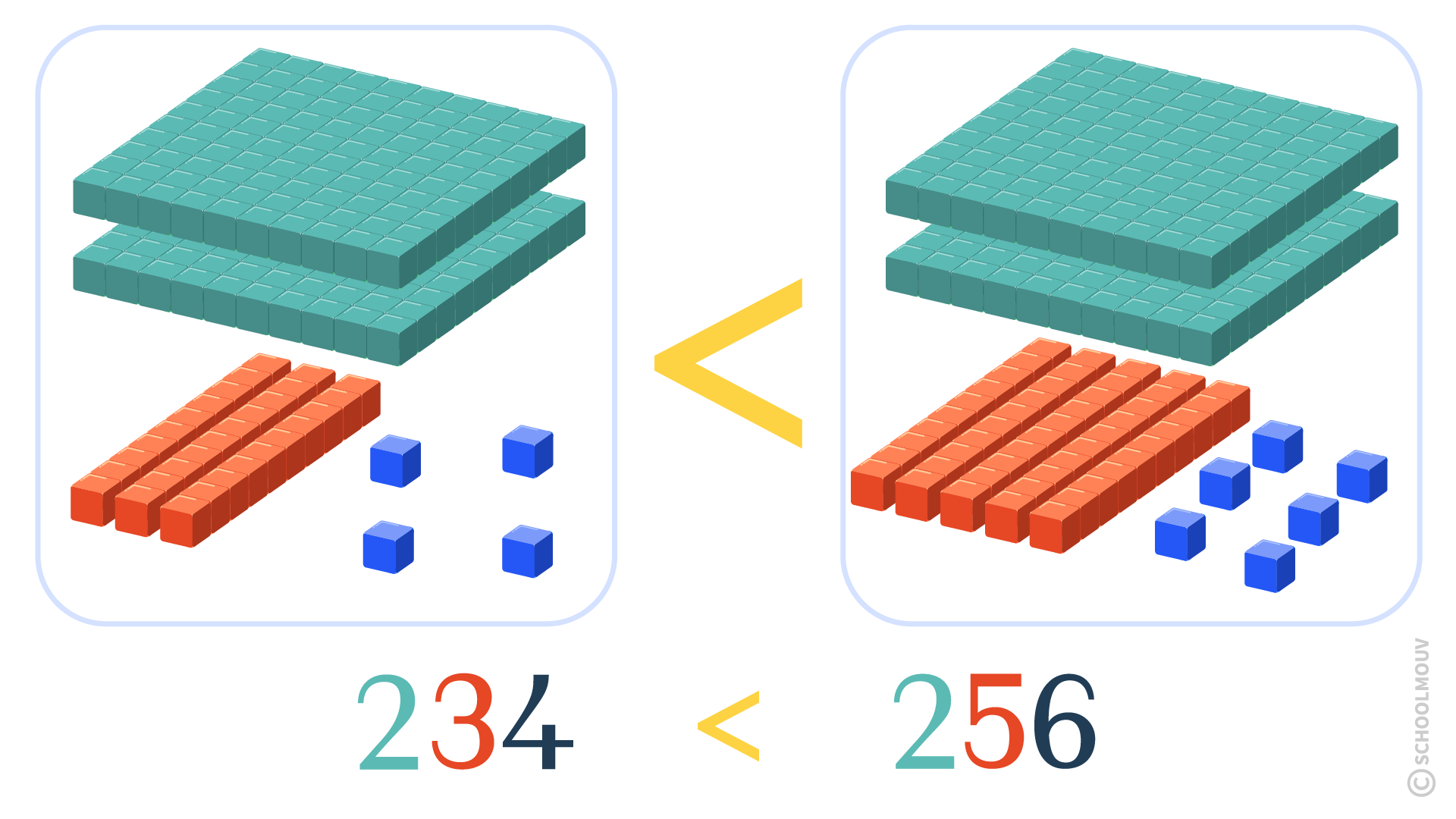
- 234 est plus petit que 256.
- si les chiffres des centaines sont identiques et si les chiffres des dizaines sont identiques, on compare les chiffres des unités.
Exemple
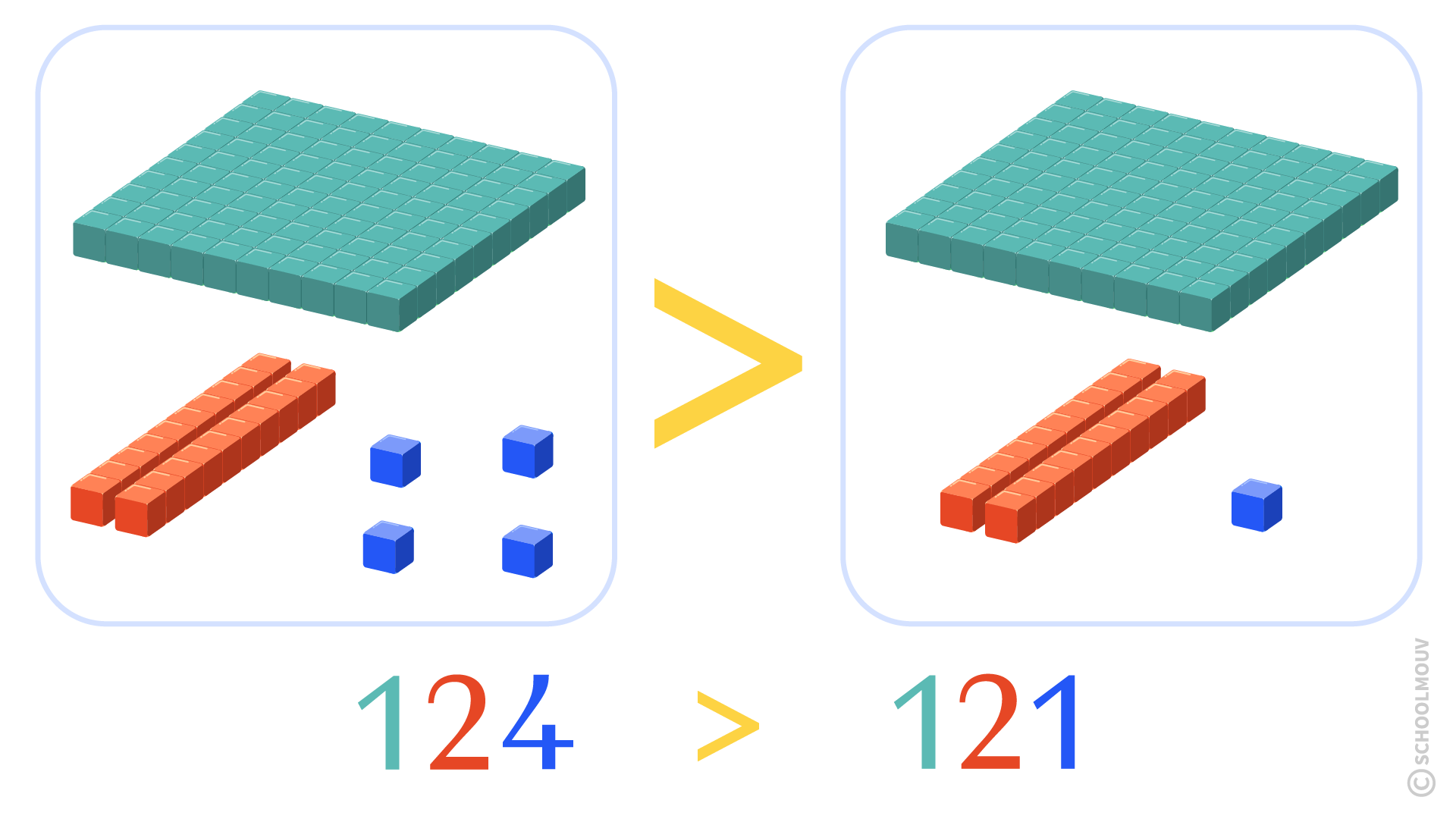
- 124 est plus grand que 121.
Ordonner des nombres
Ordonner des nombres
Pour ordonner des nombres inférieurs à 1 000, on commence par comparer les nombres, puis on peut les classer dans l’ordre croissant (du plus petit au plus grand) ou dans l’ordre décroissant (du plus grand au plus petit).
Exemple
Classons les nombres dans l’ordre croissant :
Classer des nombres dans l’ordre croissant
Classons les nombres suivants dans l’ordre décroissant :
Classer des nombres dans l’ordre décroissant
Astuce
Savoir que la pointe montre toujours le nombre le plus petit aide à se souvenir comment utiliser les signes > et<.
3 < 6
- La pointe montre le 3, c’est donc le plus petit.
7 > 4
- La pointe montre le 4, c’est donc le plus petit.