Exercices Calcul intégral

Calculer la valeur moyenne $m$ sur $[0;\pi]$ de la fonction $f$ définie par $f(x)=sin \, x$.

On définit la fonction $f$ par morceaux :

$f(x)= \left\lbrace \begin{array}{ccc} \dfrac{-1}{x^2} & \text{si} \, & 1\leqslant x < \dfrac{\pi}{2} \\ \dfrac{x \cos x-\sin x}{x^2} & \text{si} \, & \dfrac{\pi}{2} \leqslant x < \pi \\ -\dfrac1x + 2\cos x \sin x & \text{si} \, & {\pi} \leqslant x \leqslant 2\pi\end{array}\right.$

Peux-ton affirmer que la fonction $f$ est continue sur $[1;3\pi]$ ?

Question 1

On considère la fonction $f$ définie sur $\mathbb R$ par :

$$f(x)=\dfrac {2x}{x^2+\frac 34}+1$$

On admet que $f$ est continue sur $\mathbb R$ et on donne ci-dessous $\mathscr C_f$, sa courbe représentative dans un repère orthonormé :

• Étudier le signe de la fonction $f$ sur $\mathbb R$.
• On veut évaluer graphiquement la valeur de l’intégrale :

$$\int_{-0,5}^{4} f(x) \text d x$$

Parmi les propositions suivantes, laquelle est vraie ? Justifier.

• Déterminer une primitive de $f$ sur $\mathbb R$, puis trouver la valeur exacte de :

$$\int_{-0,5}^{4} f(x) \text d x$$

Question 2

On considère maintenant la fonction $g$ définie sur $\mathbb R^+$ par :

$$g(x)=2x\text{e}^{-2x+1}$$

• Prouver que, pour tout réel positif $x$ :

$$g^{\prime}(x)=2\text{e}^{-2x+1}(1-2x)$$

• Déterminer les variations de $g$ sur $\mathbb R^+$, puis construire son tableau de variations.
• On admettra que $\lim\limits_{x \to +\infty} g(x)=0$.
• Quel est le signe de $g(x)$ sur $\mathbb R^+$ ?

Question 3

Soit la suite $(I_n )$ définie, pour tout entier naturel, par :

$$I_n=\int_0^n g(x)\text{d}x$$

Par exemple :

$$\begin{aligned} I_0&=\int_0^0 g(x)\text{d}x=0 \\ I_1&=\int_0^1 g(x)\text{d}x \\ I_2&=\int_0^2g(x)\text{d}x \end{aligned}$$

• Soit $n$ un entier naturel.
  En utilisant la relation de Chasles, exprimer $I_{n+1}$ en fonction de $I_n$.
• En déduire que $I_{n+1} \geq I_n$ pour tout entier naturel $n$.
  Que peut-on dire de la suite $(I_n)$ ?

À l’aide d’une intégration par parties, on peut montrer que, pour tout entier naturel $n\geq 1$ :

$$I_n=\dfrac {\text{e}}2-\text{e}^{-2n+1}\left(n+\dfrac 12\right)\qquad \textcolor{#A9A9A9}{(1)}$$

Cette formule est également vraie pour $n=0$.

• Dans la suite de l’exercice, on admet donc que la relation $(1)$ est vraie pour tout entier naturel $n$.
  Mais, pour vous entraîner, vous pouvez faire l’intégration par parties, le détail sera donné en astuce dans le corrigé.
• Démontrer que la suite $(I_n)$ est majorée par $\frac {\text{e}}2$, puis qu’elle converge vers un réel que l’on note $l$.
• On admet que :

$$\lim\limits_{n \to +\infty} I_n=l=\dfrac {\text{e}}2$$

On a programmé en Python l’algorithme ci-dessous :

Quand on entre sur la console Python la commande $\purple{\text{approche(4)}}$, le programme renvoie la valeur $\purple{\text{7}}$. Que signifie ce résultat ?

Question 4

Une animalerie adopte le logo représenté par la figure plus bas.

• La courbe $\mathscr C_f$ est représentée sur $[-0,5\ ;\, 4]$ en trait plein vert.
• La courbe en pointillés verts est sa courbe symétrique par rapport à l’axe des abscisses.
• De même, la courbe représentant $g$ est $\mathscr C_g$, tracée en trait plein rouge.
• La courbe en pointillés rouges est sa symétrique par rapport à l’axe horizontal.

On admettra que $\mathscr C_f$ est au-dessus de $\mathscr C_g$ sur l’intervalle $[0\ ;\, 4]$.

Calculer l’aire de la partie bleue du logo, comprise entre :

• les droites d’équations $x=-0,5$ et $x=4$ ;
• les courbes $\mathscr C_f$ et $\mathscr C_g$ ;
• leurs symétriques par rapport à l’axe des abscisses.

Une entreprise vend des peluches et s’intéresse à la quantité vendue, jour après jour, au cours de l’année 2017. Elle s’aperçoit que les ventes ont suivi la courbe suivante :

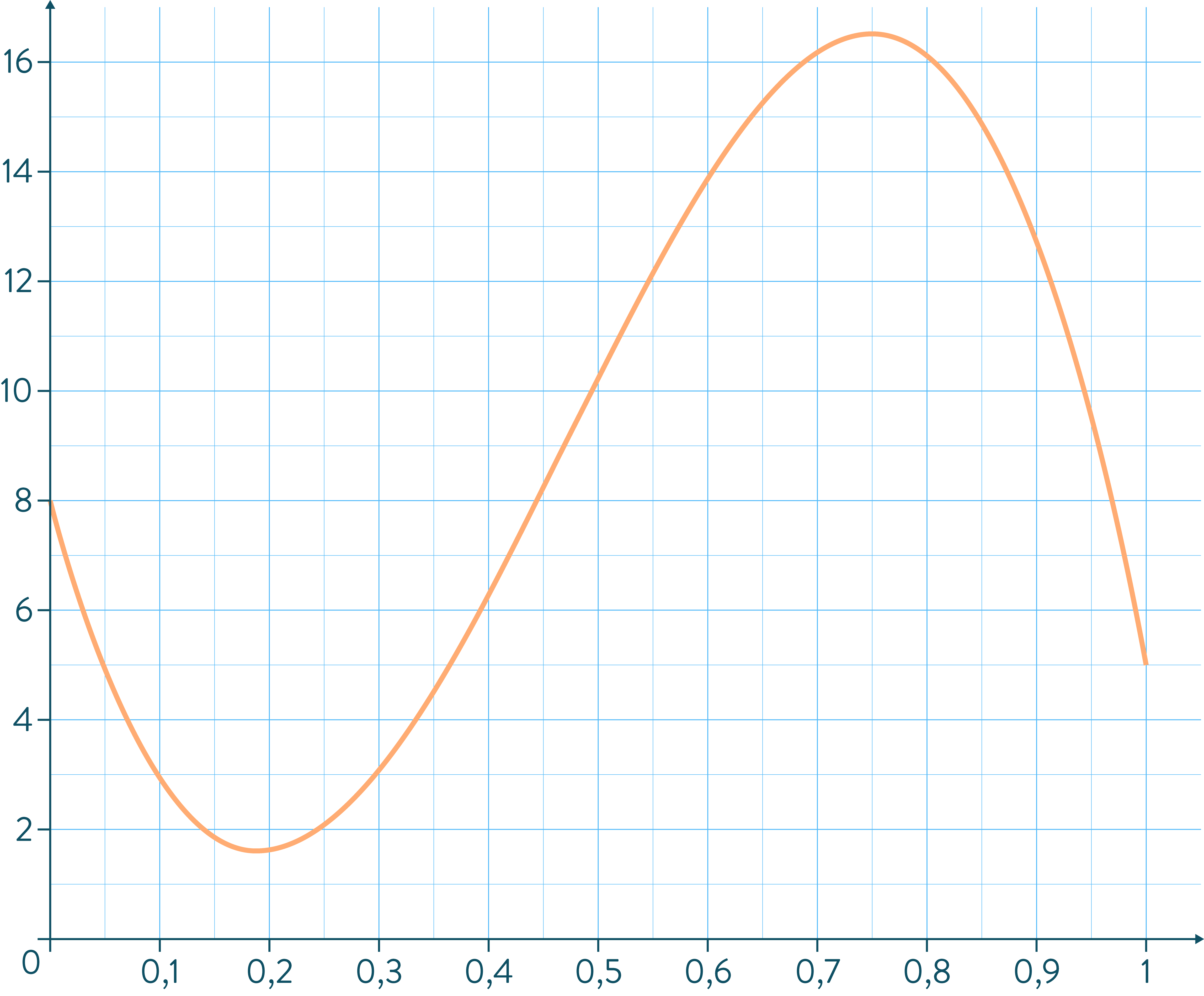
L’abscisse $0$ correspond au 1^er janvier, l’abscisse $1$ au 31 décembre de l’année 2017 (qui compte 365 jours).

Ainsi, si les jours sont numérotés de 0 à 364 (qui correspondent aux jours du 1^er janvier jusqu’au 31 décembre), le jour numéro $n$ correspond à l’abscisse $\dfrac{n}{364}$.

Par exemple, le 20 janvier 2017 c’est le jour numéro 19 donc l’abscisse $\dfrac{19}{364}\approx 0,05$ (à 0,05 près) soit une ordonnée de 5. Le graphique nous indique que le 20 janvier, l’entreprise a vendu 5 peluches.
Combien l’entreprise a-t-elle vendu de peluches (on arrondira à l’unité) au jour $n_{326}$ et à quel jour de l’année cela correspond-t-il ?

Pour cette question, on utilisera une calculatrice.