Cours Simplification des expressions logiques
Introduction :
Ici, nous allons appliquer les propriétés apprises dans le cours précédent, afin de simplifier une équation logique.
Nous verrons aussi une autre méthode, plus visuelle et rapide, pour opérer une simplification à partir d’une table de vérité.
Exemple de table de vérité
Nous l’avons vu, une table de vérité nous donne une équation logique sous sa forme canonique disjonctive. Celle-ci peut donc avoir de nombreux termes et il conviendra alors de la simplifier.
- C’est d’ailleurs ce que nous avons fait pour retrouver l’équation simplifiée de la fonction $\text{OU}$ à partir de sa table de vérité.
Pour montrer le principe, nous allons nous appuyer sur la table de vérité suivante :
$a$ |
$b$ |
$c$ |
$\red S$ |
$0$ |
$0$ |
$0$ |
$\red 0$ |
$0$ |
$0$ |
$1$ |
$\red 0$ |
$0$ |
$1$ |
$0$ |
$\red 0$ |
$0$ |
$1$ |
$1$ |
$\red1$ |
$1$ |
$0$ |
$0$ |
$\red0$ |
$1$ |
$0$ |
$1$ |
$\red1$ |
$1$ |
$1$ |
$0$ |
$\red1$ |
$1$ |
$1$ |
$1$ |
$\red1$ |
Simplification algébrique
Utilisons, d’abord, la technique que nous connaissons tous, celle algébrique, en nous appuyant sur les propriétés vues dans le cours précédent.
- Écrivons l’équation à partir de la table de vérité :
$$S=\bar a\cdot b\cdot c+a\cdot \bar b\cdot c+a\cdot b\cdot \bar c+a\cdot b\cdot c$$
- Elle est sous sa forme canonique disjonctive.
- Nous cherchons donc à la simplifier.
Dans le tableau suivant, nous indiquons chaque étape de la simplification et nous précisons la propriété appliquée.
$S=\bar a\cdot b\cdot c+a\cdot \bar b\cdot c+a\cdot b\cdot \bar c+a\cdot b\cdot c$ |
Forme canonique disjonctive |
$S=\bar a\cdot b\cdot c+\red{a\cdot (\bar b\cdot c+ b\cdot \bar c+ b\cdot c)}$ |
Distributivité : factorisation par $a$ |
$S=\bar a\cdot b\cdot c+a\cdot \big(\bar b\cdot c+ \red{b\cdot (\bar c+ c)}\big)$ |
Distributivité : factorisation par $b$ |
$S=\bar a\cdot b\cdot c+a\cdot (\bar b\cdot c+ b\cdot \red 1)$ |
$\bar c + c=1$ |
$S=\bar a\cdot b\cdot c+a\cdot \red{(b + \bar b\cdot c)}$ |
$1$ élément neutre de $\text{ET}$, puis commutativité |
$S=\bar a\cdot b\cdot c+a\cdot \red{(b + c)}$ |
Absorption : $b + \bar b\cdot c = b+c$ |
$S=\bar a\cdot b\cdot c+\red{a\cdot b + a\cdot c}$ |
Distributivité : développement |
$S=\red{c\cdot(\bar a\cdot b+a)}+a\cdot b$ |
Distributivité : factorisation par $c$ |
$S=c\cdot\red{ (a+\bar a\cdot b)}+a\cdot b$ |
Commutativité |
$S=c\cdot\red{(a+ b)}+a\cdot b$ |
Absorption : $a + \bar a\cdot b = a+b$ |
$S=a\cdot b + a\cdot c+b\cdot c$ |
Distributivité : développement, puis commutativité |
- L’expression simplifiée est donc : $S=a\cdot b + a\cdot c+b\cdot c$.
Simplification par la méthode de Karnaugh
Pour simplifier par la méthode algébrique, il faut parfois de nombreuses étapes, procéder à tâtons, sans parler du fait qu’il faut connaître toutes les propriétés (même si ce dernier point, bien sûr, ne nous pose aucun problème…).
- Rassurez-vous, il existe une méthode visuelle et plus rapide : la méthode de Karnaugh !
De la table de vérité au tableau de Karnaugh
La méthode repose sur la propriété vue et démontrée dans le cours précédent :
$$a\cdot \red b+a\cdot \red {\bar b}=a$$
Et elle consiste à identifier tous les mintermes qui ne diffèrent que par l’état d’une seule variable (appelés adjacents) : nous pourrons alors « éliminer » la variable qui change d’état.
Dans la propriété citée, seul l’état de $b$ change, nous supprimons donc la variable $b$ pour ne conserver que $a$.
Nous l’avons dit, si une fonction dépend de $n$ variables, il y aura au maximum $2^n$ mintermes.
- Nous les représentons dans un tableau de Karnaugh.
Tableau de Karnaugh :
Il s’agit d’une table de vérité particulière, à double entrée, qui présente tous les produits possibles entre les variables et leurs compléments.
- Un tel tableau comptera $2^n$ cellules.
Le lien entre le nombre de cases d’un tableau de Karnaugh et le nombre de lignes de la table de vérité associée est direct : il y a autant de produits possibles que de lignes dans la table de vérité et de cases dans le tableau de Karnaugh.
- Pour $n$ variables d’entrée, il y a $2^n$ lignes dans la table de vérité, il y a donc $2^n$ cellules à compléter dans le tableau de Karnaugh.
Si le nombre de variables $n$ est pair, les lignes représenteront les valeurs des $\frac n2$ premières variables et les colonnes les $\frac n2$ variables restantes.
Si le nombre de variables $n$ est impair, les lignes représenteront les valeurs des $\frac {n-1}2$ premières variables et les colonnes les $\frac {n+1}2$ variables restantes.
Puisqu’il s’agit d’identifier les termes où une seule variable change d’état, il est important, pour les lignes et les colonnes, de donner les valeurs des variables selon l’ordre du code de Gray, et non selon celui du code binaire naturel (comme dans une table de vérité classique).
Voici les tableaux de Karnaugh pour $2$, $3$ et $4$ variables.
Tableau à $2$ variables
$b\rightarrow$ $a\downarrow$ |
$0$ |
$1$ |
$0$ |
$\bar a\cdot \bar b$ |
$\bar a\cdot b$ |
$1$ |
$a\cdot \bar b$ |
$a\cdot b$ |
Tableau à $3$ variables
$bc\rightarrow$ $a\downarrow$ |
$00$ |
$01$ |
$11$ |
$10$ |
$0$ |
$\bar a\cdot \bar b \cdot \bar c$ |
$\bar a\cdot \bar b \cdot c$ |
$\bar a\cdot b \cdot c$ |
$\bar a\cdot b \cdot \bar c$ |
$1$ |
$a\cdot \bar b \cdot \bar c$ |
$a\cdot \bar b \cdot c$ |
$a\cdot b \cdot c$ |
$a\cdot b \cdot \bar c$ |
Tableau à $4$ variables
$cd\rightarrow$ $ab\downarrow$ |
$00$ |
$01$ |
$11$ |
$10$ |
$00$ |
$\bar a \cdot \bar b \cdot \bar c \cdot \bar d$ |
$\bar a \cdot \bar b \cdot \bar c \cdot d$ |
$\bar a \cdot \bar b \cdot c \cdot d$ |
$\bar a \cdot \bar b \cdot c \cdot \bar d$ |
$01$ |
$\bar a \cdot b \cdot \bar c \cdot \bar d$ |
$\bar a \cdot b \cdot \bar c \cdot d$ |
$\bar a \cdot b \cdot c \cdot d$ |
$\bar a \cdot b \cdot c \cdot \bar d$ |
$11$ |
$a \cdot b \cdot \bar c \cdot \bar d$ |
$a \cdot b \cdot \bar c \cdot d$ |
$a \cdot b \cdot c \cdot d$ |
$a \cdot b \cdot c \cdot \bar d$ |
$10$ |
$a \cdot \bar b \cdot \bar c \cdot \bar d$ |
$a \cdot \bar b \cdot \bar c \cdot d$ |
$a \cdot \bar b \cdot c \cdot d$ |
$a \cdot \bar b \cdot c \cdot \bar d$ |
Pour passer d’une table de vérité à un tableau de Karnaugh, il suffit d’écrire $1$ dans les cellules qui correspondent aux combinaisons ayant pour sortie $1$, et $0$ dans les cellules restantes.
Appliquons ce principe à la table de vérité donnée en début de cours :
$a$ |
$b$ |
$c$ |
$\red S$ |
$0$ |
$0$ |
$0$ |
$\red 0$ |
$0$ |
$0$ |
$1$ |
$\red 0$ |
$0$ |
$1$ |
$0$ |
$\red 0$ |
$0$ |
$1$ |
$1$ |
$\red1$ |
$1$ |
$0$ |
$0$ |
$\red0$ |
$1$ |
$0$ |
$1$ |
$\red1$ |
$1$ |
$1$ |
$0$ |
$\red1$ |
$1$ |
$1$ |
$1$ |
$\red1$ |
- Nous obtenons le tableau de Karnaugh suivant :
$bc\rightarrow$ $a\downarrow$ |
$00$ |
$01$ |
$11$ |
$10$ |
$0$ |
$0$ |
$0$ |
$1$ |
$0$ |
$1$ |
$0$ |
$1$ |
$1$ |
$1$ |
Par exemple :
- la cellule en orange ($0\ 01$, soit $\bar a\cdot \bar b\cdot c$) correspond à la deuxième ligne de la table de vérité ;
- la cellule en jaune ($1\ 11$, soit $a\cdot b \cdot c$) correspond à la dernière ligne de la table de vérité.
Simplification à partir du tableau de Karnaugh
Voyons maintenant à quoi ce tableau sert.
Par exemple, intéressons-nous aux deux cellules correspondant à $0\ 11$ et $1\ 11$.
Nous le savons, l’équation de vérité contiendra les termes : $\bar a\cdot b\cdot c + a\cdot b \cdot c$.
- Et selon la propriété d’absorption mentionnée :
$$\begin{aligned} \bar a\cdot b\cdot c + a\cdot b \cdot c&=\bar a\cdot (b\cdot c) + a\cdot (b \cdot c) \\ &= (b\cdot c)\cdot(\bar a + a) \\ &= (b\cdot c)\cdot 1 \\ &= b\cdot c \end{aligned}$$
- Nous pouvons simplifier en éliminant la variable $a$, qui est la seule changeant de valeur !
La simplification par la méthode de Karnaugh repose sur ce principe.
- Dans le tableau, nous regroupons les valeurs égales adjacentes par une puissance de $2$ ($1$, $2$, $4$, $8$, $16$, etc.).
- La dernière ligne est adjacente à la première, la dernière colonne est adjacente à la première colonne (nous le voyons : une seule variable change d’état).
- Nous veillons à ce que toutes les valeurs égales appartiennent à un groupe.
- Un terme peut participer à plusieurs groupes (car $a + a = a$).
- Dans chaque groupe, nous supprimons la ou les variables qui changent d’état.
- Si un groupe contient un seul terme, nous ne pouvons évidemment supprimer aucune variable.
- Nous écrivons le produit des variables restantes, avec leurs valeurs (qui donc ne changent pas) dans le tableau.
- Nous faisons la somme de l’ensemble des termes ainsi obtenus.
Insistons sur ce point : les termes doivent être groupés par une puissance de $2$.
- Il ne faut donc pas faire des groupes de $3$, $5$, $7$, $10$… termes !
Regardons deux tableaux de Karnaugh avec $4$ variables.

Nous regroupons les $4$ termes égaux à $1$. Dans le groupe ainsi formé :
- $a$ change de valeur ;
- $b$ ne change pas de valeur ;
- $c$ change de valeur ;
- $d$ ne change pas de valeur.
- Nous pouvons éliminer $a$ et $c$.
- L’équation logique est : $S=b\cdot \bar d$.
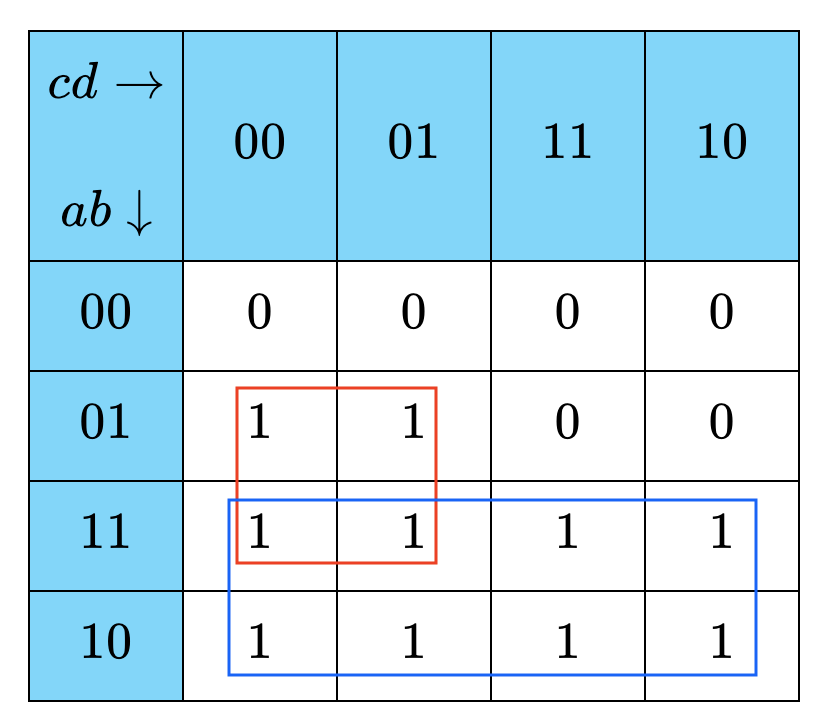
Nous pouvons ici former $2$ groupes, l’un de $4$ termes, l’autre de $8$ termes.
- Dans le premier groupe (encadré en rouge), $a$ et $d$ changent de valeur.
Nous écrivons le terme correspondant : $b\cdot \bar c$.
- Dans le deuxième groupe (encadré en bleu), seul $a$ ne change pas de valeur.
Nous écrivons le terme correspondant : $a$.
- D’où l’équation logique : $S=a+b\cdot \bar c $.
Pour terminer, reprenons le tableau de Karnaugh constitué à partir de la table de vérité prise en exemple :

Nous constituons $3$ groupes de $2$ termes.
- Pour celui encadré en bleu, seul $a$ change de valeur : $b\cdot c$.
- Pour celui encadré en rouge, seul $b$ change de valeur : $a\cdot c$.
- Pour celui encadré en vert, seul $c$ change de valeur : $a\cdot b$.
- D’où l’équation logique : $S=a\cdot b+a\cdot c+b\cdot c$.
- Ce qui correspond bien à ce que nous trouvions avec la simplification algébrique, mais nous y sommes parvenus de manière plus visuelle !
Conclusion :
Vous l’avez vu, l’algèbre de Boole est régie par des lois proches de celle que vous manipulez depuis longtemps.
Apprendre les formules, bien sûr, mais, en réalité, il ne s’agit que de logique, donc faites travailler votre bon sens et peut-être qu’une lumière s’allumera !
Ainsi pouvez-vous retrouver comment tout cela fonctionne et manipuler les portes logiques même si elles sont nombreuses et qu’elles dépendent de nombreuses variables. Comme dans un microprocesseur, par exemple !





