Cours Variable aléatoire et loi de probabilité
Introduction :
Ce cours commence avec la définition d’une variable aléatoire, avant celle de la loi de probabilité d’une telle variable.
Puis nous passerons aux définitions de l’espérance, de la variance et de l’écart-type d’une loi de probabilité, avant d’étudier une variable aléatoire pour voir si elle est équitable, c’est-à-dire d’espérance nulle.
Enfin, la troisième partie sera consacrée à un exemple qui concerne la répétition de deux expériences identiques et indépendantes.
Variable aléatoire et loi de probabilité
Rappels de vocabulaire
- Une expérience est dite aléatoire lorsqu’elle a plusieurs résultats possibles et qu’on ne peut pas prévoir celui qui sera obtenu. Le résultat d’une telle expérience est uniquement dû au hasard.
- Chaque résultat possible d’une expérience aléatoire est appelé issue de cette expérience.
- L’ensemble des issues d’une expérience aléatoire s’appelle l’univers de l’expérience.
- Un événement de cette expérience est un sous-ensemble de son univers.
- Un événement élémentaire de cette expérience est un événement contenant une seule issue.
Exemple :
L’expérience qui consiste à lancer un dé équilibré à $6$ faces et à noter le numéro inscrit sur la face supérieure est une expérience aléatoire.
- L’univers de l’expérience est l’ensemble $\Omega=\lbrace1\ ;\,2\ ;\,3\ ;\,4\ ;\,5\ ;\,6\rbrace$.
- L’événement $A$ : « Obtenir un résultat pair », est l’ensemble $A=\lbrace2\ ;\,4\ ;\,6\rbrace$.
- L’événement élémentaire $B$ : « Obtenir un 6 », est l’ensemble $B=\lbrace 6\rbrace$.
Variable aléatoire
Variable aléatoire :
On considère une expérience aléatoire dont l’univers est un ensemble fini noté $\Omega$.
- Une variable aléatoire $X$ est une fonction définie sur $\Omega$ à valeurs dans $\mathbb R$.
Définir une variable aléatoire consiste donc à associer un réel à chaque issue de l’expérience aléatoire.
Exemple :
Un joueur lance un dé équilibré à $6$ faces :
- s’il obtient $1$, $2$ ou $3$, il perd $5$ euros ;
- s’il obtient $4$ ou $5$, il gagne $1$ euro ;
- s’il obtient $6$, il gagne $10$ euros.
- On peut définir la variable aléatoire $X$ égale au gain algébrique du joueur.
$\Omega$ est l’ensemble des issues et $X(\Omega)$ l’ensemble des valeurs prises par la variable aléatoire $X$.
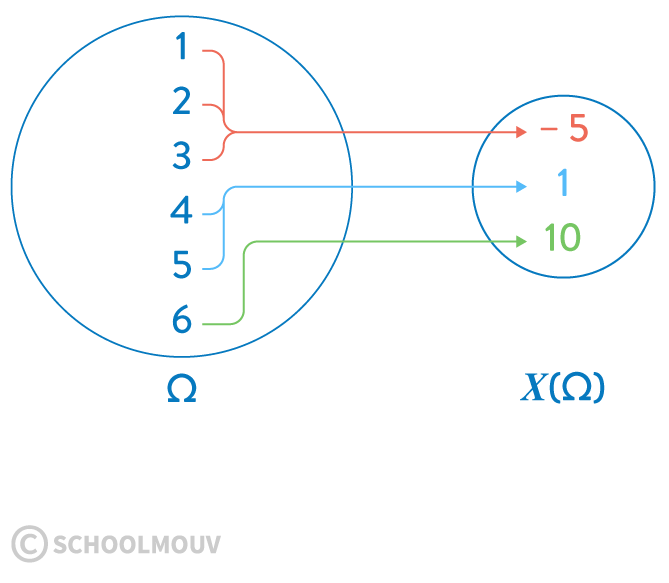
Loi de probabilité d’une variable aléatoire
Loi de probabilité d’une variable aléatoire :
Soit $X$ une variable aléatoire discrète sur $\Omega$ qui prend les valeurs $x_1,\,x_2,\,…\ ,\,x_k$.
Définir la loi de probabilité de $X$, c’est donner les valeurs de probabilités $p(X=x_i)$ pour tout entier $i$, avec $1\leq i\leq k$.
On présente en général une loi de probabilité sous forme d’un tableau :
Valeur $x_i$ prise par $X$ |
$x_1$ |
$x_2$ |
… |
$x_k$ |
Probabilité $p(X=x_i)$ |
$p_1=p(X=x_1)$ |
$p_2=p(X=x_2)$ |
… |
$p_k=p(X=x_k)$ |
Dans le tableau qui donne la loi de probabilité d’une variable aléatoire, la somme des probabilités est égale à $1$ :
$\begin{aligned} p_1+p_2+…+p_k&=\displaystyle\sum_{i=1}^{k} p(X=x_i) \\ &=1 \end{aligned}$
Exemple :
On lance un dé équilibré à $6$ faces :
- on gagne $2$ euros si le résultat est $5$ ou $6$ ;
- on gagne $1$ euro si le résultat est $4$ ;
- on perd $1$ euro sinon.
- On appelle $G$ la variable aléatoire égale au gain algébrique du joueur en fin de partie.
Pour établir la loi de probabilité de $G$, on doit d’abord trouver les valeurs prises par la variable aléatoire $G$.
Ici, le joueur peut obtenir :
- $5$ ou $6$, et dans ce cas le gain algébrique est de $2$ euros ;
- $4$, et dans ce cas le gain algébrique est de $1$ euro ;
- $1$, $2$ ou $3$, et dans ce cas le gain algébrique est de $-1$ euro.
- $G(\Omega)=\lbrace -1\ ;\,1\ ;\,2\rbrace$
- Une fois les valeurs prises par $G$ trouvées, on doit calculer les probabilités correspondantes :
$\begin{aligned} p(G=-1)&=\dfrac{3}{6} \\ &=\dfrac{1}{2} \\ p(G=1)&=\dfrac{1}{6} \\ p(G=2)&=\dfrac{2}{6} \\ &=\dfrac{1}{3} \end{aligned}$
On peut toujours vérifier en faisant la somme des probabilités. On sait que le résultat doit être égal à $1$.
$\begin{aligned} p(G=-1)+p(G=1)+p(G=2)&=\dfrac{3}{6}+\dfrac{1}{6}+\dfrac{2}{6} \\ &=\dfrac{6}{6} \\ &=1 \end{aligned}$
- La loi de probabilité de $G$ est donc :
$g_i$ |
$-1$ |
$1$ |
$2$ |
$p(G=g_i)$ |
$\dfrac{1}{2}$ |
$\dfrac{1}{6}$ |
$\dfrac{1}{3}$ |
- Si on souhaite calculer la probabilité $p(G\leq1)$, on doit calculer :
$\begin{aligned} p(G\leq 1)&=p(G=-1)+p(G=1) \\ &=\dfrac{3}{6}+\dfrac{1}{6} \\ &=\dfrac{4}{6} \\ &=\dfrac{2}{3} \end{aligned}$
- On peut aussi calculer cette probabilité à l’aide de l’événement contraire (le gain est strictement supérieur à $1$ euro seulement lorsqu’il est égal à $2$ euros) :
$\begin{aligned} p(G\leq1)&=1-p(G>1) \\ &=1-p(G=2) \\ &=1-\dfrac{1}{3} \\ &=\dfrac{2}{3} \end{aligned}$
Indicateurs d’une variable aléatoire
Espérance, variance, écart-type
Espérance mathématique :
L’espérance mathématique de la variable aléatoire $X$ est le réel noté $E(X)$ défini par :
$\begin{aligned} E(X)&=x_1\times p_1+x_2\times p_2+…+x_k\times p_k \\ &=\displaystyle\sum_{i=1}^{k}x_ip_i \end{aligned}$
L’espérance d’une variable aléatoire $X$ s’interprète comme la valeur moyenne prise par $X$ lorsqu’on répète un très grand nombre de fois l’expérience.
Exemple :
Reprenons l’exemple précédent :
$g_i$ |
$-1$ |
$1$ |
$2$ |
$p(G=g_i)$ |
$\dfrac{1}{2}$ |
$\dfrac{1}{6}$ |
$\dfrac{1}{3}$ |
- Calculons l’espérance mathématique de la variable aléatoire $G$.
$\begin{aligned} E(G)&=g_1p_1+g_2p_2+g_3p_3 \\ &=-1\times\dfrac{1}{2}+1\times\dfrac{1}{6}+2\times\dfrac{1}{3} \\ &=-\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{2}{3} \\ &=-\dfrac{3}{6}+\dfrac{1}{6}+\dfrac{4}{6} \\ &=\dfrac{2}{6} \\ &=\dfrac13 \\ &\approx0,33 \end{aligned}$
On peut interpréter le résultat de la manière suivante :
- si un joueur participait $100$ fois à ce jeu, c’est-à-dire un grand nombre de fois, son « gain » total serait d’environ : $100\times0,33\approx33$ euros ;
- ainsi, sur 100 parties, le joueur gagnerait environ $33$ euros.
Variance d’une variable aléatoire :
La variance de la variable aléatoire $X$ est le réel positif noté $V(X)$ défini par :
$\begin{aligned} V(X)&=p_1×\big(x_1-E(X)\big)^2+p_2×\big(x_2-E(X)\big)^2+… \\ &+p_k×\big(x_k-E(X)\big)^2 \\ &=\displaystyle\sum^{k}_{i=1}p_i\big(x_i-E(X)\big)^2 \end{aligned}$
Exemple :
Reprenons encore une fois l’exemple précédent où l’on avait trouvé $E(G)=\dfrac{1}{3}$.
$g_i$ |
$-1$ |
$1$ |
$2$ |
$p(G=g_i)$ |
$\dfrac{1}{2}$ |
$\dfrac{1}{6}$ |
$\dfrac{1}{3}$ |
- Calculons la variance de la variable aléatoire $G$.
$\begin{aligned} V(G)&=\dfrac{1}{2}\times\Big(-1-\dfrac{1}{3}\Big)^2+\dfrac{1}{6}\times\Big(1-\dfrac{1}{3}\Big)^2+\dfrac{1}{3}\times\Big(2-\dfrac{1}{3}\Big)^2 \\ &=\dfrac{1}{2}\times\dfrac{16}{9}+\dfrac{1}{6}\times\dfrac{4}{9}+\dfrac{1}{3}\times\dfrac{25}{9} \\ &=\dfrac{48}{54} + \dfrac{4}{54} +\dfrac{50}{54} \\&= \dfrac{102}{54} \\ &=\dfrac{17}{9} \\ &\approx1,89 \end{aligned}$
Écart-type :
L’écart-type $\sigma(X)$ est défini comme la racine carrée de la variance :
$\sigma(X)= \sqrt{V(X)}$
La lettre grecque $\sigma$ se lit sigma.
La variance et l’écart-type mesurent la dispersion des valeurs prises par $X$ autour de $E(X)$.
- Plus la variance et l’écart-type sont grands, plus les valeurs sont dispersées.
Jeu équitable
Maintenant que l’on sait calculer l’espérance d’une variable aléatoire, il est intéressant de l’appliquer aux exercices, de manière à analyser l’expérience aléatoire et se demander si elle équitable.
Jeu équitable :
$\Omega$ est l’ensemble des issues d’un jeu de hasard.
$X$ est la variable aléatoire définie sur $\Omega$ qui est égale au gain du joueur.
- Dire que ce jeu est équitable signifie que $E(X)=0$.
Exemple :
Un ticket de jeu à gratter coûte $2$ euros.
On considère l’expérience aléatoire qui consiste à tirer au hasard un ticket de ce jeu parmi l’ensemble des tickets disponibles.
$X$ est la variable aléatoire qui donne le gain du joueur, en tenant compte du prix d’achat du ticket.
Ce gain peut aussi être négatif.
- La loi de probabilité de la variable aléatoire $X$ est donnée dans le tableau ci-dessous :
Gain $x_i$ (en euros) |
$-2$ |
$0$ |
$3$ |
$8$ |
$18$ |
$48$ |
$198$ |
$p(X=x_i)$ |
$0,6$ |
$0,2173$ |
$0,1205$ |
$0,0485$ |
$0,0124$ |
$0,0012$ |
$0,0001$ |
- L’espérance de la variable aléatoire $X$ est :
$\begin{aligned} E(X)=\big(0,6\times(-2)\big)&+(0,2173\times0)+(0,1205\times 3)+(0,0485\times 8) \\ &+(0,0124\times 18)+(0,0012\times 48)+(0,0001\times 198) \\ \end{aligned}$
$\begin{aligned} E(X)&=-1,2+0,3615+0,388+0,2232+0,0576+0,0198 \\ &=-0,1499\\ \end{aligned}$
- $E(X)\neq0$, donc ce jeu n’est pas équitable.
- $E(X)<0$, donc ce jeu est défavorable au joueur.
Répétition d’expériences identiques et indépendantes
Expériences identiques et indépendantes, arbre pondéré
Expériences aléatoires identiques et indépendantes :
Deux expériences aléatoires sont considérées comme identiques et indépendantes si elles ont les mêmes issues et les mêmes probabilités, et si la réalisation de l’une ne modifie pas les probabilités des issues de l’autre.
Exemple :
Je lance un premier dé équilibré et j’observe la face supérieure, puis je lance un second dé équilibré.
- Ces deux expériences aléatoires sont identiques et indépendantes.
Pour modéliser une situation d’expériences répétées indépendantes, on utilise un arbre pondéré.
Sur un arbre pondéré :
- la somme des probabilités des branches issues d’un même nœud est $1$ ;
- la probabilité d’un chemin est le produit des probabilités rencontrées le long de ce chemin ;
- la probabilité d’un événement est la somme des probabilités des chemins menant à cet événement.
Exemple de résolution
Voyons comment un arbre pondéré permet d’étudier une variable aléatoire.
Dans un jeu de $32$ cartes, on tire $1$ carte, et on regarde s’il s’agit d'une figure. On la remet dans le jeu, qu'on mélange, puis on en tire $1$ autre.
On appelle $Y$ la variable aléatoire égale :
- à $30$ si on tire $2$ figures ;
- à $20$ si on tire une figure et une autre carte qui n’est pas une figure ;
- à $10$ sinon.
- L’objectif est de déterminer la loi de probabilité de la variable aléatoire $Y$.
- Pour cela, commençons par construire un arbre pondéré.
- On note $F$ l’événement : « Tirer une figure ».
- L’événement $\bar F$ est l’événement contraire de $F$, c’est-à-dire : « Tirer une carte qui n’est pas de figure ».
Comme on effectue deux tirages, il faut construire un arbre pondéré à deux niveaux.
Dans un jeu de $32$ cartes, il y a $12$ figures, donc :
$\begin{aligned} p(F)&=\dfrac{12}{32} \\ & =\dfrac{3}{8} \\ p(\bar F)&=1-\dfrac{12}{32} \\ &=\dfrac{20}{32} \\ &=\dfrac{5}{8} \end{aligned}$

Pour chaque chemin, on note la correspondance avec la loi de probabilité :
- Lisons maintenant l’arbre.
- L’événement : « Obtenir deux figures », est réalisé par le premier chemin $F\cap F$, au bout duquel on note donc : $Y=30$.
- L’événement : « Obtenir une figure et une carte qui n’est pas une figure », est réalisé par deux chemins $F\cap\bar F$ et $\bar F\cap F$, au bout desquels on note donc : $Y=20$.
- L’événement : « Ne pas obtenir de figure » est réalisé par le dernier chemin $\bar F\cap\bar F$, au bout duquel on note donc : $Y=10$.

- D’après les propriétés de calcul avec un arbre pondéré, on obtient :
$\begin{aligned} p(Y=30)&=p(F\cap F) \\ &=\dfrac{3}{8}\times\dfrac{3}{8} \\ &=\dfrac{9}{64} \\ p(Y=20)&=p(F\cap\bar F)+p(\bar F\cap F) \\ &=\dfrac{3}{8}\times\dfrac{5}{8}+\dfrac{5}{8}\times\dfrac{3}{8} \\ &=\dfrac{15}{64}+\dfrac{15}{64} \\ &=\dfrac{30}{64} \\ &=\dfrac{15}{32} \\ p(Y=10)&=p(\bar F\cap \bar F) \\ &=\dfrac{5}{8}\times\dfrac{5}{8} \\ &=\dfrac{25}{64} \end{aligned}$
- On obtient la loi de probabilité suivante pour $Y$ :
$y_i$ |
$10$ |
$20$ |
$30$ |
$p(Y=y_i)$ |
$\dfrac{25}{64}$ |
$\dfrac{15}{32}$ |
$\dfrac{9}{64}$ |
- L’espérance mathématique de la variable aléatoire $Y$ est :
$\begin{aligned} E(Y)&=y_1p_1+y_2p_2+y_3p_3 \\ &= 10\times\dfrac{25}{64}+20\times\dfrac{15}{32}+30\times\dfrac{9}{64} \\ &=\dfrac{250}{64}+\dfrac{600}{64}+\dfrac{270}{64} \\ &=\dfrac{1\,120}{64} \\ &= 17,5 \end{aligned}$
- La variance de la variable aléatoire $Y$ est :
$\begin{aligned} V(Y)&=\dfrac{25}{64}\times(10-17,5)^2+\dfrac{15}{32}\times(20-17,5)^2+\dfrac{9}{64}\times(30-17,5)^2 \\ &=\dfrac{25}{64}\times(-7,5)^2+\dfrac{15}{32}\times2,5^2+\dfrac{9}{64}\times(12,5)^2 \\ &=\dfrac{25}{64}\times56,25+\dfrac{15}{32}\times6,25+\dfrac{9}{64}\times156,25 \\ &=\dfrac{1\,406,25+187,5+1\,406,25}{64} \\ &=\dfrac{3\,000}{64} \\ &=46,875 \end{aligned}$
- L’écart-type de la variable aléatoire $Y$ est :
$\begin{aligned} \sigma(Y)&=\sqrt{V(Y)} \\ &=\sqrt{46,875} \\ &\approx6,85 \end{aligned}$




