Exercices Probabilités conditionnelles et indépendance

Sur tous les candidats inscrits au bac 2015 :

• $49\ \%$ étaient inscrits à un bac dit général, $20\ \%$ à un bac dit technologique et les autres à un bac dit professionnel ;
• $91,5\ \%$ des candidats au bac général ont été reçus, comme $90,6\ \%$ des candidats au bac technologique.

On choisit au hasard un candidat au bac 2015 et on considère les événements suivants :

• $G$ : le candidat était inscrit à un bac général,
• $T$ : le candidat était inscrit à un bac technologique,
• $P$ : le candidat était inscrit à un bac professionnel,
• $R$ : le candidat a été reçu.

Donner les valeurs de $p(G)$, $p(T)$, $p_G (R)$, $p_T (R)$.

Dans le groupe il y a des enfants originaires du village de Vintiblanc (dont $20\ \%$ pratiquent le ski) et des enfants originaires de Déciblanc (dont $10\ \%$ pratiquent le ski).
En prévision d’une classe de neige, on désigne un capitaine de groupe à qui on met un foulard autour du cou.
Le capitaine n’est pas obligé de pratiquer du ski.
Pour le désigner, on tire un foulard au hasard dans un sac contenant 10 foulards dont  foulards marqués $V$ et  foulards marqués $D$.
Si le foulard est marqué $V$, on choisit un enfant de Vintiblanc et il sera le capitaine, par contre si le foulard tiré au sort est marqué $D$, on choisit un enfant de Déciblanc et on le désigne capitaine.
On note respectivement $V$ et $D$ les événements le capitaine est de Vintiblanc (respectivement de Déciblanc), et l’on note $S$ l’événement le capitaine pratique le ski.
On arrondira éventuellement les résultats à $1\ \%$ près.

Quelle est la probabilité, sachant que le capitaine est de Vintiblanc, d’avoir un capitaine qui pratique le ski ?

On lance une pièce truquée (la probabilité de pile est $p \in ]0;1[$ ). Si on obtient pile, on choisit une voyelle au hasard dans l'alphabet, sinon une consonne. On rappelle que les voyelles sont {A,E,I,O,U,Y}. On note M l'événement : « la lettre choisie est dans le mot DETERMINANT », V l'événement « on a obtenu pile » et C l'événement « on a tiré face ».

On suppose qu'on a obtenu pile. Quelle est la probabilité que la lettre choisie soit dans le mot « DETERMINANT » ?

Dans un groupe mixte, 20 % de filles parlent espagnol et 10 %des garçons parlent espagnol). On tire un foulard au hasard dans une urne contenant 30 foulards bleus et 20 foulards rouges. On accroche le foulard au cou d'une fille tirée au sort si c'est un foulard rouge, d'un garçon tiré au sort si c'est un foulard bleu. La personne portant le foulard sera capitaine de soirée. On note respectivement F et G les événements « le capitaine de soirée est une fille » et «  le capitaine de soirée est un garçon », et l'on note E l'événement « le capitaine de soirée parle espagnol ».

Quelle est la probabilité, sachant que le capitaine de soirée est une fille, d'avoir un capitaine de soirée qui parle espagnol ?
On arrondira éventuellement les résultats à 1 % près.

Pour les vacances, un animateur propose aux enfants de faire du basket ou d’aller à la piscine. Tous les matins, chaque enfant choisit l’activité qu’il va suivre pendant la journée. Le premier jour, $20\ \%$ des enfants ont choisi pasket et tous les autres ont choisi piscine. On admet que :

• $20\ \%$ des enfants ayant choisi piscine un certain jour s’inscrivent au basket le lendemain ;
• $30\ \%$ des enfants ayant choisi basket un certain jour s’inscrivent en piscine le lendemain.

On s’intéresse à l’effectif de chaque groupe au fil des jours.
Chaque matin, on interroge un enfant au hasard. Pour tout entier $n$, on note $A_n$ l’événement cet enfant a choisi basket le n-ième jour et $B_n$ l’événement contraire, cet enfant a choisi piscine le n-ième jour.
On a donc $p_1=0,2$.

Compléter de même les autres pointillés.

Compléter l’arbre du problème :

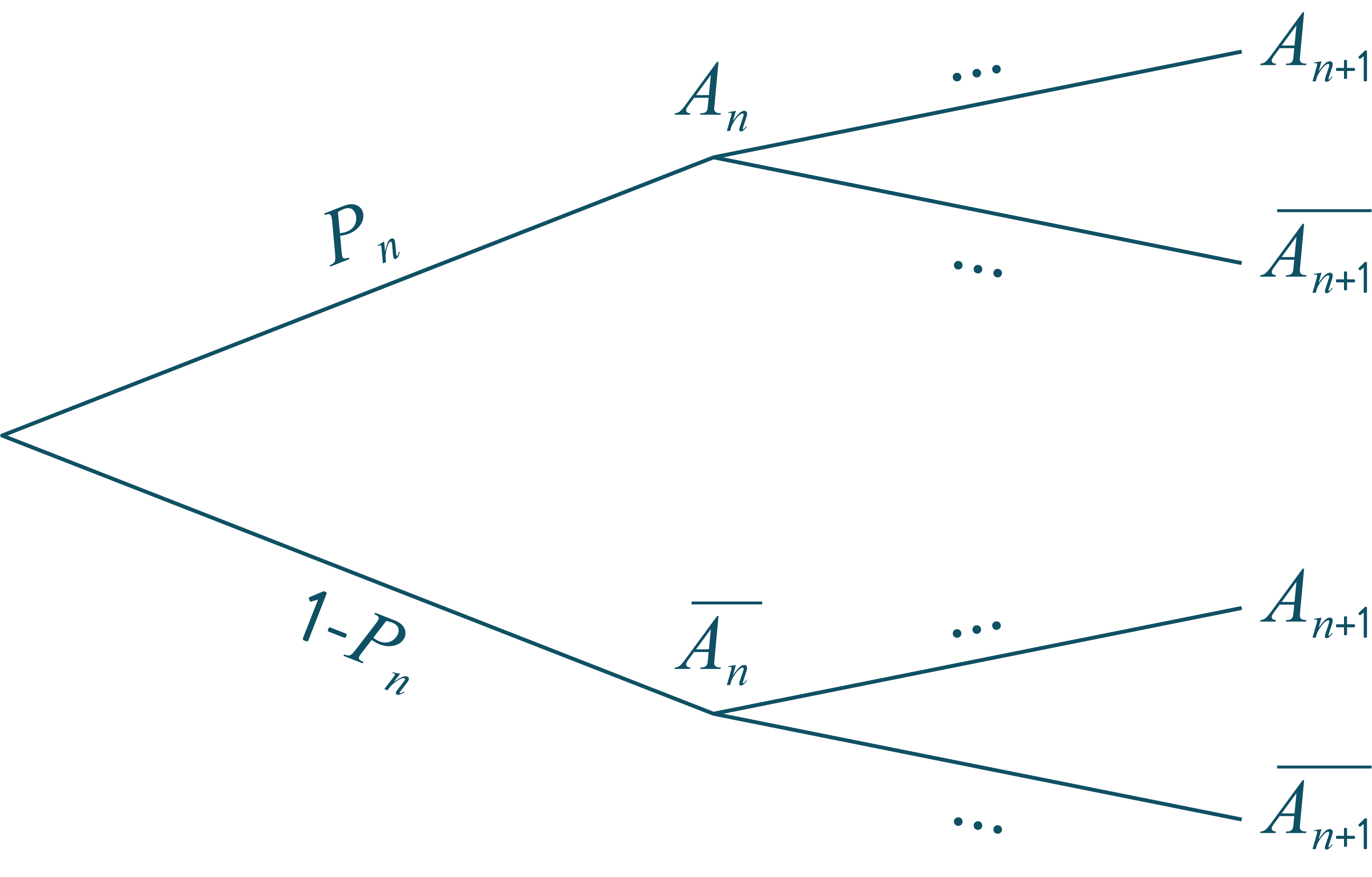
Quand je fais une série de lancers francs au basket, je réussis toujours mon premier panier. Ensuite, si je réussis un lancer, la probabilité que je réussisse le suivant est 0,6, mais si je rate un lancer, cela me démotive et la probabilité que je rate le suivant est 0,9. On note $R_n$ l'événement : « le $n$-ième lancer est réussi » et $p_n=(R_n)$.

Calculer la probabilité des événements A et B suivants :

• A : le second et le troisième paniers sont réussis ;
• B : le second et le troisième paniers sont ratés.